Эллипс

Кривые второго порядка. Эллипс, гипербола и парабола, их свойства и канонические уравнения. Приведение уравнения второго порядка к каноническому виду.

Лекция 11.

Определение 11.1. Кривыми второго порядка на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.

Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс, при пересечении образующих обеих полостей – гипербола, а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола.

Замечание. Все кривые второго порядка задаются уравнениями второй степени от двух переменных.

Определение 11.2. Эллипсом называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F ₁ и F ₂ этой плоскости, называемых фокусами, есть величина постоянная.

Замечание. При совпадении точек F ₁ и F ₂ эллипс превращается в окружность.

Выведем уравнение эллипса, выбрав декартову систему

у М(х,у) координат так, чтобы ось Ох совпала с прямой F ₁ F ₂, начало

r₁ r₂ координат – с серединой отрезка F ₁ F ₂. Пусть длина этого

отрезка равна 2 с, тогда в выбранной системе координат

F₁ O F₂ x F ₁(- c, 0), F ₂(c, 0). Пусть точка М(х, у) лежит на эллипсе, и

сумма расстояний от нее до F ₁ и F ₂ равна 2 а.

Тогда r ₁ + r ₂ = 2 a, но ,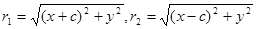

поэтому 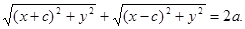Введя обозначение b ² = a ²- c ² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса: 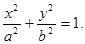(11.1)

Определение 11.3. Эксцентриситетом эллипса называется величина е=с/а (11.2)

Определение 11.4. Директрисой D_i эллипса, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а/е от начала координат.

Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (11.1), а уравнением второй степени другого вида.

Свойства эллипса:

1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2 а и 2 b (2 a >2 b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

2) Весь эллипс содержится внутри прямоугольника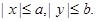

3) Эксцентриситет эллипса e < 1.

Действительно,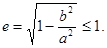

4) Директрисы эллипса расположены вне эллипса (так как расстояние от центра эллипса до директрисы равно а/е, а е <1, следовательно, а/е>a, а весь эллипс лежит в прямоугольнике )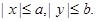

5) Отношение расстояния r_i от точки эллипса до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.

Доказательство.

Расстояния от точки М(х, у) до фокусов эллипса можно представить так:

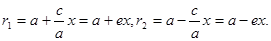Составим уравнения директрис:

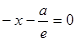(D ₁), 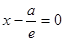(D ₂). Тогда 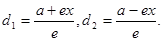Отсюда r_i / d_i = e, что и требовалось доказать.

Дата добавления: 2014-01-11