Производные и дифференциалы высших порядков, их свойства. Точки экстремума функции. Теоремы Ферма и Ролля

Лекция 19.

Пусть функция y=f(x) дифференцируема на некотором отрезке [ ab ]. В таком случае ее производная представляет собой тоже некоторую функцию х. Продифференцировав эту функцию, мы получим так называемую вторую производную (или производную второго порядка) функции f(x). Продолжая эту операцию, можно получить производные третьего, четвертого и более высоких порядков. При этом f`(x) будем называть производной первого порядка.

Определение 19.1. Производной n -го порядка (или n -й производной) от функции f(x) называется производная (первого порядка) от ее (n- 1)-й производной.

Обозначение: у⁽ⁿ⁾=(y^{(n- 1 )} )΄=f⁽ⁿ⁾(x). Производные 2-го и 3-го порядка обозначаются соответственно y′΄ и y΄′΄.

Примеры.

1) Найдем производную 3-го порядка от функции y=x³-5x²+3x+12.

y΄=3x²-10x+3, y΄΄=(y΄)΄=6x-10, y΄΄΄=(y΄΄)΄=6.

2) Получим общую формулу для производной n -го порядка функции y=a^bx.

y΄=a^bx·lna·b, y΄΄=lna·b(a^bx)΄=a^bx·ln²a·b²,…, y⁽ⁿ⁾=a^bx·lnⁿa·bⁿ.

Свойства производных высших порядков.

Основные свойства производных высших порядков следуют из соответствующих свойств первой производной:

1. (cf(x))⁽ⁿ⁾=c·f⁽ⁿ⁾(x).
2. (f(x)+g(x))⁽ⁿ⁾=f⁽ⁿ⁾(x)+g⁽ⁿ⁾(x).
3. Для y=x^m y⁽ⁿ⁾=n(n- 1 )…(n-m+ 1 )x^m-n. Если m – натуральное число, то при n>m y⁽ⁿ⁾=0.
4. Можно вывести так называемую формулу Лейбница, позволяющую найти производную n -го порядка от произведения функций f(x)g(x):

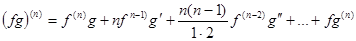. (19.1)

Заметим, что коэффициенты в этой формуле совпадают с соответствующими коэффициентами формулы бинома Ньютона, если заменить производные данного порядка той же степенью переменной. Для n =1 эта формула была получена при изучении первой производной, для производных высших порядков ее справедливость можно доказать с помощью метода математической индукции.

1. Получим формулу для второй производной функции, заданной параметрически. Пусть x = φ(t), y = ψ(t), t₀ ≤ t ≤ T. Тогда 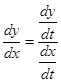. Следовательно,

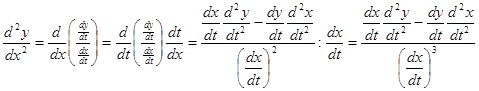(19.2)

Дата добавления: 2014-01-11