Основы асимметричных систем

АСИММЕТРИЧНЫЕ КРИПТОГРАФИЧЕСКИЕ СИСТЕМЫ

Одной из основных проблем в практическом использовании рассмотренных систем шифрования является проблема распределения секретных ключей между абонентами и проблема хранения этих ключей.

Если в системе имеется N абонентов, то для обеспечения секретного обмена информацией между любыми двумя абонентами потребуется сгенерировать и распределить N(N–1)/2 секретных ключей, причем каждый абонент вынужден будет хранить N–1 секретный ключ для обмена информацией с остальными абонентами.

Решить проблему распределения ключей помогает использование асимметричных криптографических систем. В этих системах для обмена данными используются два ключа, один из которых является секретным, а другой — открытым, т.е. общедоступным.

По этой причине асимметричные системы называются также д вухключевыми.

Все асимметричные криптографические системы основаны на использовании односторонних функций с секретом.

Определение. Функция F: X Y называется односторонней, если выполняются следующие два условия:

1) существует эффективный алгоритм, вычисляющий F(x) для любого 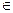x X;

2) не существует эффективного алгоритма инвертирования функции F, т.е. алгоритма, позволяющего определить значение x по значению F(x).

В данном определении «эффективным» называется полиномиальный алгоритм, т.е. алгоритм, который для получения результата для входа длины n тратит не более P(n) шагов, где P — некоторый полином.

В настоящее время теория алгоритмов не позволяет доказать не существование эффективных алгоритмов решения той или иной задачи. Поэтому, строго говоря, не известна ни одна односторонняя функция.

Однако предложено несколько функций, которые могут оказаться односторонними — для этих функций в настоящее время, несмотря на интенсивные исследования, не известны эффективные алгоритмы инвертирования.

Наиболее часто используются «односторонние» функции, заимствованные из теории чисел:

• Функция F(a, b) = ab, то есть произведение двух чисел. Если a и b — простые числа, то по известному c = ab можно однозначно определить a и b. Эта задача называется задачей факторизации числа. До сих пор не известен ни один полиномиальный алгоритм для решения задачи факторизации, хотя для вычисления произведения чисел (т.е. самой функции F) такие алгоритмы известны.

• Функция F(a, n) = 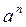(mod M), где a, n и M — целые числа. При известных a, n и M значение b = 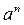(mod M) может быть вычислено за полиномиальное количество шагов. Однако для обратной задачи — определить n по известным a, b и M (задача дискретного логарифмирования) — полиномиальные алгоритмы, в общем случае, пока не известны.

Не любая односторонняя функция может быть использована для шифрования. Действительно, если преобразовать открытый текст t с помощью односторонней функции: c = F(t), то расшифровать полученный текст, то есть по

c восстановить t, не сможет уже никто, в том числе и законный получатель. Для использования в криптографии необходимо, чтобы задача инвертирования шифрующего преобразования ( т.е. вычисления t по F(t)) была разрешима за приемлемое время, но сделать это мог только тот, кто знает секретный ключ.

Такие функции называются односторонними функциями с секретом

(или с потайным ходом).

Определение. Односторонняя функция с секретом — это функция 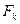:X Y, зависящая от параметра k 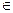K (этот параметр называется секретом), для которой выполняются следующие условия:

1) при любом k 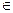K существует эффективный алгоритм, вычисляющий Fk( x) для любого 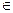x X;

2) при неизвестном k не существует эффективного алгоритма инвертирования функции ;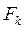

3) при известном k существует эффективный алгоритм инвертирования функции .

Существование односторонних функций с секретом, как и существование односторонних функций, пока не доказано. Однако известны функции, которые могут оказаться односторонними функциями с секретом, если будет доказано, что

инвертирование этих функций действительно является сложной задачей.

Рассмотрим в общем виде принцип использования односторонних функций с секретом для шифрования сообщений. Каждый абонент криптосистемы выбирает некоторую одностороннюю функцию 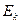с секретом k. Функции 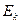всех

абонентов заносятся в общедоступный справочник, но значение секрета k каждый абонент, как и следует из названия, держит в секрете.

Если абонент B хочет переслать сообщение t абоненту A, он извлекает из справочника функцию 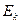абонента A и с ее помощью вычисляет c = 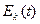. Шифртекст c пересылается абоненту A, который по нему вычисляет исходное сообщение t, инвертировав функцию 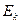с помощью секрета k. Расшифроватьсообщение может только абонент A, поскольку кроме него никто не знает секрет k.

Примечание. Обычно функции шифрования 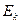для разных абонентов вычисляются по одному и тому же заранее установленному алгоритму, но в зависимости от некоторого параметра p. У каждого абонента параметр p собственный. Этот параметр называется открытым ключом данного абонента,

поэтому асимметричные криптосистемы называют также криптосистемами с открытым ключом.

В качестве примера рассмотрим процедуру открытого распределения ключей и криптосистему RSA.

Дата добавления: 2014-01-11