Процедура открытого распределения ключей

Как указывалось, одной из наиболее сложных проблем в применении криптографических систем является распределение секретных ключей между абонентами. При использовании классических, т.е. симметричных, систем шифрования, для распределения ключей необходимо устанавливать специальный

канал, полностью защищенный от возможной атаки противника.

Асимметричные криптографические системы позволяют распределять секретные ключи по открытым каналам, т.е. каналам, которые потенциально могут быть прослушаны противником. Такая процедура открытого распределения ключей была впервые опубликована в 1976 году в работе У. Диффи и Э. Хеллмана «Новые направления в криптографии».

В основе процедуры Диффи –Хеллмана лежит использование односторонней функции дискретного возведения в степень:

F(x) = g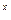(mod p), (2)

где x — целое число (1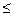x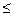p–1), p — простое число, g — первообразный корень по модулю p.

Определение. Первообразным корнем по модулю p называется такое целое число g (g < p), для которого:

1) все степени g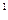(mod p), g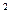(mod p), …, g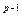(mod p) различны;

2) для любого целого числа a, такого что 1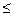a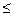p–1, найдется n, при котором a = g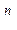(mod p).

Возводя число g в степени 1, 2, …, p–1(по модулю p), получим все числа от 1 до p–1, образующие Zp * (мультипликативную группу кольца Zp). Поэтому такое число g называется также генератором группы Zp *.

Процедура Диффи –Хеллмана для открытого распределения ключей заключается в следующем. Для начала выбирается большое простое число p и число g — первообразный корень по модулю p.

Для обеспечения стойкости число p должно иметь длину, большую или равную 512 бит, и разложение числа p–1 на множители должно содержать хотя бы один большой простой множитель (например, p–1 = 2q, где q — простое число). Здесь и далее длиной целого числа будем называть количество бит в двоичной записи этого числа.

При таком выборе числа p в настоящее время не существует эффективного алгоритма для решения задачи инвертирования функции (2).

Каждый абонент в качестве своего секретного ключа выбирает некоторое случайное число x, по которому вычисляет свой открытый ключ y = g 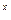(mod p). Все абоненты помещают свои открытые ключи в общедоступный справочник.

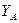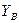После этого, если два абонента, A и B, захотят обменяться секретным сообщением, они берут из общедоступного справочника открытые ключи друг друга (соответственно, и) и вычисляют общий секретный ключ:

1) абонент A вычисляет

2) абонент B вычисляет

Таким образом, после выполнения описанной процедуры у абонентов A и B есть общее число = 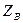. Это число они при обмене сообщениями могут использовать в качестве ключа для шифрования (например, методом гаммирования).

Противник знает числа = 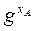(mod p) и 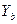= 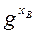(mod p), но для того чтобы определить секретный ключ, ему необходимо решить задачу дискретного логарифмирования (по известным 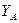и 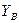вычислить 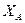и 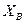). Как уже отмечалось раньше, для этой задачи в настоящее время не существует эффективного алгоритма.

Дата добавления: 2014-01-11