Криптосистема RSA

Криптосистема RSA названа по первым буквам фамилий разработавших ее специалистов — Ривеста (R. Rivest), Эдлмана (L. Adleman). Эта система используется как для шифрования данных, так и для формирования цифровой подписи.

Опишем процедуру шифрования с помощью системы RSA, а затем дадим ее математическое обоснование. В системе RSA каждый абонент формирует для себя секретный и открытый ключ следующим образом:

1. Выбирает два больших, неравных между собой, простых числа n = pq и m = (p–1)(q–1).

2. Выбирает целое число е, такое, что e < m и НОД (e, m) = 1 (то есть число е должно быть взаимно просто с m).

3. Выбирает число d, удовлетворяющее условию: ed = 1 (mod m)

4. Секретным ключом абонента является тройка чисел (p, q, d), а открытым ключем пара чисел (n, e).

5. Открытые ключи всех абонентов помещаются в общедоступный справочник.

Примечание. Существование числа d, удовлетворяющего условию шага 3, что следует из теоремы Евклида: “Для b найдутся целые числа x и y, такие, что ax + by = НОД (a,b) ”. Расширенный алгоритм Евклида позволяет эффективно вычислить это число d.

Алгоритмы для построения больших (длиной 512 и более бит) простых чисел для нахождения числа e, удовлетворяющего условию сложны для понимания.

Функция шифрования сообщения, представленного в виде числа t ( t<n) в системе RSA определяется формулой: E(t) = t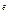(mod n).

Функция расшифрования (зависящая от секретного ключа) задается формулой: D(c) = c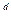(mod n).

Длинное сообщение разбивается на блоки длиной 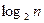(чтобы каждый блок представлял собой число, меньшее n). Каждый блок шифруется, и затем расшифровывается, отдельно.

Проверим, что функция E(t) действительно является односторонней функцией с секретом.

Свойство 1 из определения односторонней функции с секретом выполняется, поскольку для возведения в степень (в том числе и по определенному модулю) существуют эффективные алгоритмы.

Свойство 2 пока строго не доказано. Считается, что для инвертирования функции E необходимо определить число d, а для этого надо вычислить m, что невозможно без разложения числа n на простые множители p и q.

Для доказательства свойства 3 надо убедиться, что функция D действительно является обратной к функции E, то есть что для любого числа t выполняется D(E(t)) = t.

Доказательство основано на теореме Эйлера из теории чисел: “Для любых взаимно простых целых чисел a и n выполняется соотношение”:

a 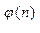= 1 (mod n), где:

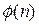— функция Эйлера, равная количеству целых чисел, больших 0 и меньших n, и взаимно простых с n. Для n=pq, где p и q — простые, 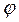( n) = (p–1)(q–1), то есть 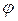(n) в точности равно выбранному нами параметру m. Поскольку n равно произведению двух больших простых чисел, любое произвольно выбранное число t взаимно просто с n с вероятностью, практически равной 1.

Докажем, что функция D обратна к функции E:

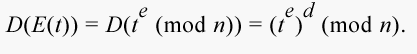
Числа e и d выбраны так, что выполняется условие ed = 1(mod 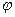(n)). Это равносильно тому, что существует целое число r, такое, что ed = r 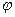(n) + 1. Поэтому

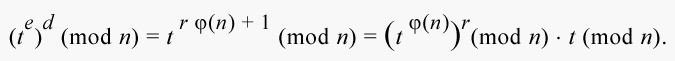
Воспользовавшись теоремой Эйлера, получим:

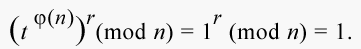
Следовательно, мы доказали, что для любого t, меньшего n, выполняется: D(E(t)) = t (mod n) = t.

Особенности использования асимметричных криптосистем на практике

По эффективности и стойкости асимметричные (двухключевые) системы проигрывают симметричным (одноключевым) — при одинаковой длине ключа лучшие асимметричные процедуры шифрования работают медленнее и обеспечивают меньшую секретность, чем лучшие симметричные шифры. Поэтому обычно асимметричные системы используют для шифрования не самостоятельно, а в комплексе с симметричными системами. Например, шифрование данных с помощью симметричного (одноключевого) алгоритма 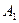и асимметричного (двухключевого) алгоритма 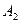выполняется в следующем

порядке:

1) Генерируется случайный ключ 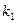для алгоритма .

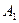2) С помощью этого ключа производится шифрование данных: c’ = .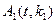

3) Ключ 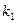шифруется с помощью алгоритма 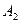на открытом ключе

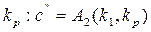
4) Шифртекст представляет собой пару c=(c', c'').

Для того чтобы расшифровать полученное сообщение (c', c''), получатель по c'' восстанавливает ключ 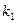, с помощью которого затем по c' расшифровывает исходный текст.

Поскольку длина ключа 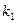невелика по сравнению с длиной текста, подобная схема дает значительный выигрыш в скорости.

Примечание. Стойкость асимметричных систем основана на предположении о существовании односторонних функций. Это предположение пока не доказано, хотя и не опровергнуто. В результате развития теории алгоритмов могут быть получены эффективные методы решения задач, использующихся в асимметричных криптосистемах (например, задачи дискретного логарифмирования), и тогда такие системы перестанут быть стойкими, а все зашифрованные с их помощью документы смогут быть расшифрованы. Но даже если будет доказано отсутствие эффективных алгоритмов для решения таких задач, асимметричные системы все равно останутся только вычислительно стойкими, т.е. их взлом будет теоретически возможным, хотя и будет требовать больших временных и вычислительных ресурсов. Абсолютно стойкие системы шифрования есть только в классе симметричных систем.

Асимметричные системы нашли также широкое применение в криптографических протоколах, позволяя решать задачи, не сводящиеся к «классическому» шифрованию: цифровая подпись, аутентификация и т.д.

Дата добавления: 2014-01-11