Постановка задачи. Разбиение системы на звенья

Математическое описание линейных автоматических систем управления

Структурная схема системы

При создании автоматической системы управления могут возникнуть разные по своему содержанию задачи: в одном случае система может быть задана, включая значения параметров, и задача сводится к определению ее свойств; в другом случае, заданы свойства, которыми должна обладать система, т.е. указаны предъявляемые к ней требования и необходимо создать систему, удовлетворяющую этим требованиям.

Чтобы решить любую из указанных задач необходимо иметь математическое описание системы.

Математическое описание системы начинается с разбиения ее на звенья и описания этих звеньев. Математическое описание может осуществляться либо аналитически в виде уравнений, связывающих входные и выходные координаты звена, либо графически в виде характеристик, описывающих ту же связь. По уравнениям или характеристикам отдельных звеньев составляются уравнения или характеристики системы в целом, на основании которых и исследуется система.

При рассмотрении принципа действия АСУ было введено понятие “функциональная схема”. В функциональной схеме система разбита на звенья, исходя из выполняемых ими функций, т.е. назначения. Для математического описания системы её разбивают на звенья по другому принципу, а именно – из удобства получения этого описания. Для этого систему следует разбивать на возможно более простые звенья, но вместе с тем необходимо, чтобы они обладали направленностью действия. В результате при разбиении системы на звенья направленного действия математическое описание каждого такого звена может быть составлено без учета связей его с другими звеньями. Соответственно математическое описание всей системы в целом может быть получено как совокупность составленных независимо друг от друга уравнений или характеристик отдельных звеньев, образующих систему, дополненных уравнениями связей между звеньями. В результате разбиения АСУ на звенья направленного действия и получения их математического описания составляется структурная схема системы. Структурная схема системы состоит из прямоугольников, изображающих звенья, и стрелок, соединяющих выходы и входы звеньев согласно связям между ними в системе. Стрелками показываются также внешние воздействия, приложенные к отдельным звеньям системы. Каждому звену структурной схемы придается описывающее его уравнение или характеристика. При этом уравнение обычно записывается прямо на схеме внутри изображающего звено прямоугольника.

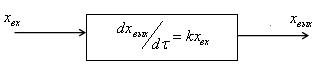
Рисунок 2.1– Изображение звена на структурной схеме.

Математическое описание может быть выполнено как для установившегося состояния, так и для неустановившегося состояния (переходного режима).

Уравнения, составленные для установившегося состояния, называют уравнениями статики, а их графическое изображение – статическими характеристиками.

Уравнения, составленные для переходного режима, называются уравнениями динамики. Представление зависимостей между выходными и входными координатами в переходном режиме на графиках называют динамическими характеристиками.

Дата добавления: 2014-01-11