Дифференциальные уравнения элементов автоматических систем

Исследование системы автоматического регулирования или ее элементов связано с изучением процессов, протекающих как в самой системе, так и в элементах. Характер и направление протекания процессов соответствуют тем или иным физическим законам, математическая формулировка которых для рассматриваемой системы и определяет уравнение, которое может быть положено в основу анализа.

Работу любой автоматической системы в переходном режиме можно описать, использовав дифференциальные уравнения, которые применимы для описания многих явлений природы и, в частности, процессов преобразования и передачи массы или энергии. А именно эти процессы и происходят в каждой автоматической системе независимо от ее принципа действия, конструктивного оформления и назначения.

Однако при описании работы систем с помощью дифференциальных уравнений возникает ряд трудностей, обусловленных спецификой автоматических систем. Прежде, чем составлять дифференциальное уравнение системы, необходимо разобраться в принципе ее действия и на основании этого составить функциональную схему системы, т.е. представить систему в виде взаимно связанных элементов, каждый из которых выполняет свою функцию. Далее, для каждого элемента системы следует составить дифференциальное уравнение динамики, связывающее выходную координату с входными. Количество таких уравнений должно равняться числу зависимых переменных, что является необходимым (но недостаточным) признаком правильности составления уравнений. Затем, исключив промежуточные переменные, можно, наконец, получить одно дифференциальное уравнение, в котором независимыми переменными являются внешние воздействия и время, а зависимой переменной – управляемая координата или ошибка системы.

Основная сложность, которая существует при выводе уравнений звеньев системы, заключается в необходимости установления допустимой степени идеализации и упрощения звеньев. Главным упрощением, к которому следует стремиться при выводе уравнений звеньев системы, является их линеаризация, т.е. получение описания линейными дифференциальными уравнениями.

В общем случае, линеаризация применима только для малых отклонений, т.е. полученные в результате линеаризации уравнения пригодны для приближенного исследования только таких режимов в системах, при которых переменные величины на входе звеньев претерпевают достаточно малые отклонения от установившихся значений. При этом точность исследования растет с уменьшением отклонений.

Во-вторых, поскольку такая линеаризация основана на разложении в ряд Тейлора, она применима только к непрерывно дифференцируемым функциям. Поэтому такие нелинейности называются линеаризуемыми. Нелинейные звенья, не удовлетворяющие этому требованию, называются существенно нелинейными.

Рассмотрим несколько примеров составления дифференциальных уравнений.

Пример № 1. Составим дифференциальное уравнение для бака с водой (рис. 2.11), который является промежуточной емкостью в системе питания водой потребителей. Для данного звена выходной координатой является уровень воды в баке, а входной – разность расходов на притоке и стоке.

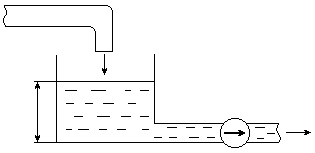
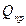
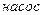
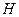
Рисунок 2.11 – Бак с водой

Для составления дифференциального уравнения воспользуемся материальным балансом. При нарушении равновесия между притоком и стоком произойдет изменение объема воды в баке, определяемое по формуле:

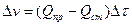(2.33)

С другой стороны,

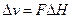(2.34)

где 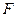– поперечное сечение бака.

Приравнивая правые части уравнений, получим

(2.35)

или

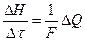(2.36)

Переходя к пределу, получим дифференциальное уравнение

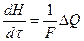(2.37)

Пример № 2. Составим дифференциальное уравнение электродвигателя постоянного тока с независимым возбуждением и малой электромеханической инерцией (рис. 2.12), у которого входной координатой является напряжение 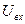, а выходной – угол поворота якоря .

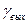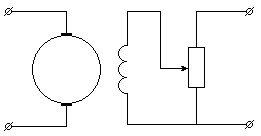
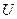
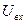
Рисунок 2.12 – Электродвигатель постоянного тока

При изменении напряжения якоря двигателя на величину изменение числа оборотов двигателя в единицу времени пропорционально :

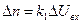(2.38)

Увеличение угла поворота якоря двигателя за бесконечно малый отрезок времени 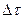пропорционально изменению числа оборотов за этот отрезок времени:

(2.39)

Подставив из уравнения (2.38) значение , получим дифференциальное уравнение двигателя:

(2.40)

или

(2.41)

где .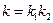

Пример № 3. Составим дифференциальное уравнение для термоэлектрического термометра, погруженного в печь с температурой , которая является входной координатой термометра, а выходной – его температура 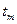(рис. 2.13). Для составления дифференциального уравнения воспользуемся тепловым балансом.

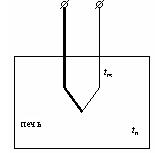
Рисунок 2.13 – Термоэлектрический термометр

Количество тепла, которое получит термометр при изменении его температуры от до 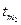, определяется по формуле:

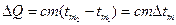(2.42)

где 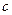– теплоемкость термометра;

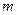– его масса.

С другой стороны, количество тепла, которое печь отдает термометру, можно определить по формуле:

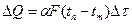(2.43)

где a - коэффициент теплопередачи;

F – поверхность, воспринимающая тепло.

Приравнивая правые части уравнений (2.42) и (2.43), получим:

(2.44)

или

(2.45)

Пример № 4. Составим дифференциальное уравнение для электрической цепочки (рис. 2.14), входной координатой которой является напряжение 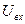, подводимое к этой цепочке, а выходной – напряжение , снимаемое с конденсатора.

Рисунок 2.14 – Электрическая цепочка

На основании второго закона Кирхгофа имеем:

(2.46)

Окончательно получим:

(2.47)

Подводя итоги, сделаем выводы:

- дифференциальное уравнение можно составить, воспользовавшись материальным или тепловым балансом, или каким-либо законом физики;

- процессы, протекающие в различных по своей конструкции и принципу действия устройствах, описываются идентичными уравнениями, т.е. динамические свойства таких устройств одинаковы;

- дифференциальное уравнение позволяет найти реакцию устройства на воздействие любого вида;

- из дифференциального уравнения легко получить уравнение статики. Для этого необходимо все производные приравнять к нулю.

Дата добавления: 2014-01-11