Передаточная функция

Рассмотрение уравнений, полученных в предыдущем разделе, показывает, что: во-первых, они очень громоздки: только переписывание их при дальнейших преобразованиях потребует много времени; во-вторых, их нельзя сразу отнести к какому-либо типовому звену, с которыми познакомимся в следующем разделе; в-третьих, в них переменные имеют определенную размерность, поэтому такие уравнения применимы для описания только рассмотренных элементов.

Мы же имели намерения получить такие уравнения, которые позволили бы описывать процессы в любой автоматической системе независимо от ее назначения и принципа действия. Поэтому уравнения отдельных элементов системы целесообразно записывать в какой-либо другой, более удобной общей форме.

Предположим, что дифференциальное уравнение системы имеет следующий вид:

(2.48)

где 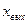– выходная координата системы;

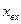– входная координата системы;

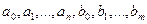– постоянные коэффициенты.

Если в уравнение (2.48) вместо функций времен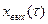и и 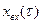ввести функци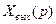и и 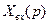комплексного переменного , поставив условием, что эти функции связаны зависимостями

(2.49)

(2.50),

то оказывается, что дифференциальное уравнение, содержащее функци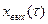и и 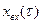при нулевых начальных условиях 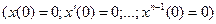, равносильно алгебраическому, содержащему функци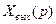и и .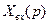

Такой переход от дифференциального уравнения к однозначно соответствующему ему алгебраическому уравнению называется преобразованием Лапласа.

Функция 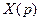называется изображением функции 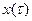. Функция 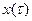называется оригиналом функции .

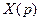Операция перехода от искомой функции 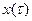к ее изображению 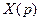называется прямым преобразованием Лапласа. Математически прямое преобразование Лапласа записывается условно с помощью символа L как

(2.51)

Формально переход от дифференциального уравнения к алгебраическому относительно изображения при нулевых начальных условиях, обычных для большинства АСР, получается путем замены символов дифференцирования оригиналов функций 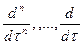соответственно на 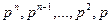и функций 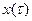– их изображениями .

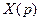Запишем дифференциальное уравнение в изображениях:

(2.52)

Полученное уравнение является алгебраическим и называется записью дифференциального уравнения в операторной форме. С оператором 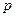, как и с другими членами алгебраического уравнения, можно производить различные действия: умножение, деление, вынесение за скобки и т.д.

Преобразование дифференциальных уравнений по Лапласу позволяет свести задачу решения системы дифференциальных уравнений к решению системы алгебраических уравнений. Определив из алгебраического уравнения изображение 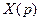искомой функции 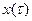, определяющей переходный процесс в системе, находят эту функцию, пользуясь таблицами оригиналов и их изображений (табл.1).

Таблица №1 - Примеры преобразований Лапласа

Оригинал	Изображение

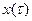
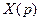
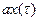
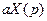
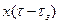
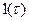
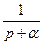
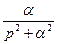
Преобразование дифференциальных уравнений по Лапласу дает возможность ввести чрезвычайно удобное понятие передаточной функции, характеризующей динамические свойства любого элемента системы. С помощью передаточных функций расчет АСР еще более упрощается и становится доступным широкому кругу инженерно-технических работников, не требуя применения сложного математического аппарата.

Вынесем в уравнении (2.52) 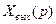и 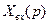за скобки:

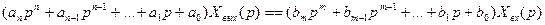(2.53)

Определим из уравнения отношение изображения выходной координаты к изображению входной:

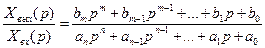(2.54)

Отношение изображения выходной координаты звена (системы) к изображению его входной координаты при нулевых начальных условиях называется передаточной функцией и обозначается .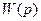

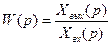(2.55)

Из уравнения (2.55) следует, что передаточная функция элемента и изображение его входной координаты определяют изображение выходной координаты:

(2.56)

Пример. Дифференциальное уравнение элемента имеет вид:

(2.57)

Записать передаточную функцию.

(2.58)

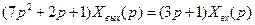(2.59)

(2.60)

Подведем некоторые итоги:

- передаточная функция – это иная запись дифференциального уравнения;

- передаточная функция – это динамический коэффициент передачи элемента системы или системы в целом (сравните );

- передаточная функция представляет собой дробно-рациональную функцию комплексной переменной р;

- коэффициенты передаточной функции являются вещественными числами;

- передаточная функция не имеет физического смысла;

- из передаточной функции легко получить уравнение статики: для этого необходимо вместо 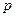подставить ноль.

Дата добавления: 2014-01-11