Реальное дифференцирующее звено и его свойства

Звено называют реальным дифференцирующим, если сумма выходной координаты и скорости ее изменения прямо пропорциональна скорости изменения входной координаты.

Дифференциальное уравнение такого звена имеет вид:

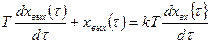(3.24)

В этом уравнении Т – постоянная времени, характеризующая инерционность процессов, протекающих в звене, а к – коэффициент передачи.

Запишем передаточную функцию звена. Для этого запишем уравнение (3.24) в операторной форме при нулевых начальных условиях:

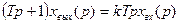
откуда

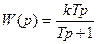(3.25)

Переходную функцию звена получим, решив уравнение (3.24) при 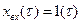. Для определения переходной функции воспользуемся преобразованием Лапласа. Так как изображение переходной функции равно передаточной функции деленной на р, то имеем:

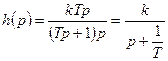(3.26)

Переходя к оригиналу, получим:

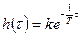(3.27)

Переходная характеристика звена приведена на рисунке 3.13.

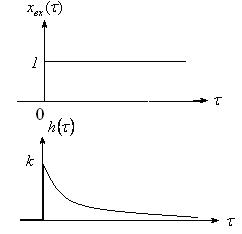
Рисунок 3.13– Переходная характеристика реального дифференцирующего звена

Определим частотные характеристики реального дифференцирующего звена, подставив jω вместо р в передаточную функцию:

(3.28)

Определим АЧХ:

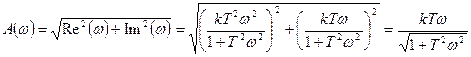(3.29)

Определим ФЧХ:

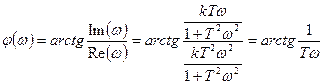(3.30)

АФХ в показательной форме будет иметь вид:

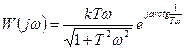(3.31)

Графики АЧХ, ФЧХ и АФХ приведены на рисунках 3.14, 3.15 и 3.16.

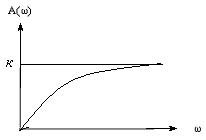
Рисунок 3.14 – Амплитудно-частотная характеристика реального

дифференцирующего звена

Рисунок 3.15 – Фазо – частотная характеристика реального

дифференцирующего звена

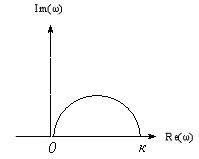
Рисунок 3.16 – Амплитудно – фазовая характеристика реального

дифференцирующего звена

Пример реального дифференцирующего звена приведен на рисунке 3.17. Чтобы убедиться, что приведенное звено является реальным дифференцирующим звеном, составим его дифференциальное уравнение. На основании второго закона Кирхгофа имеем:

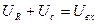(3.32)

Продифференцируем записанное уравнение по времени:

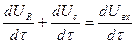(3.33)

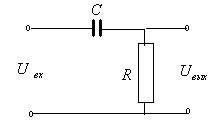
Рисунок 3.17 – Пример реального дифференцирующего звена

Учитывая, что

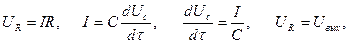получим

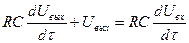(3.34)

Дата добавления: 2014-01-11