Колебательное звено и его свойства

Звено называют колебательным, если его выходная координата при единичном ступенчатом изменении входной координаты с колебаниями приходит к новому установившемуся состоянию.

Дифференциальное уравнение этого звена имеет вид:

(3.37)

где к – коэффициент передачи звена;

Т – постоянная времени;

ξ – коэффициент демпфирования (торможения).

Запишем передаточную функцию звена. Для этого запишем уравнение (3.37) в операторной форме при нулевых начальных условиях:

откуда

(3.38)

Давайте проанализируем, почему это звено называют колебательным. В знаменателе передаточной функции стоит многочлен второго порядка, который можно разложить на множители. Для этого необходимо решить характеристическое уравнение. Характеристическое уравнение это знаменатель передаточной функции, приравненный к нулю, т.е.

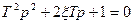(3.38)

Перепишем это уравнение в таком виде

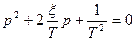(3.39)

Найдем корни уравнения (3.39)

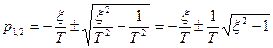(3.40)

Корни уравнения (3.39) будут различными в зависимости от подкоренного выражения в уравнении (3.40). Здесь будут наблюдаться три случая:

1) 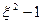>0, т.е. ξ > 1

В этом случае корни характеристического уравнения отрицательные, действительные и разные: Решение дифференциального уравнения (3.37) при единичном ступенчатом изменении входной координаты приобретает вид:

(3.41)

Из полученного уравнения видно, что при τ, стремящемся к бесконечности, выходная координата будет стремиться к новому установившемуся состоянию монотонно, не совершая колебаний, так как в этом случае рассматриваемое звено можно представить как соединение двух апериодических звеньев с разными постоянными времени (рис. 3.18).

2) 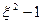=0, т.е. ξ = 1

В этом случае корни характеристического уравнения отрицательные, действительные и равные: . Решение дифференциального уравнения (3.37) при единичном ступенчатом изменении входной координаты приобретает вид:

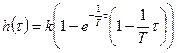(3.42)

Из полученного уравнения видно, что при τ, стремящемся к бесконечности, выходная координата опять будет стремиться к новому установившемуся состоянию монотонно, не совершая колебаний, так как в этом случае рассматриваемое звено можно представить как соединение двух апериодических звеньев с одинаковыми постоянными времени (рис. 3.19).

3) 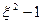<0, т.е. ξ < 1

В этом случае корни характеристического уравнения комплексно-сопряженные с отрицательной действительной частью.

(3.43)

Решение дифференциального уравнения (3.37) при единичном ступенчатом изменении входной координаты приобретает вид:

(3.44)

или

(3.45),

где

Из уравнения (3.45) видно, что выходная координата стремится к новому установившемуся значению, совершая колебания вокруг этого значения (рис.).

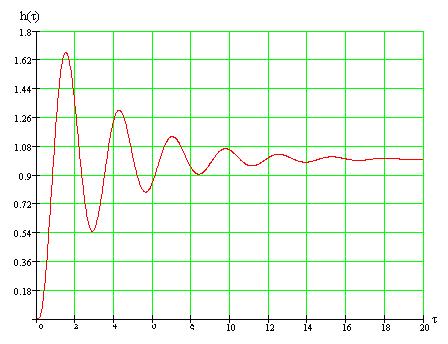
Рисунок 3.19 – Переходная характеристика колебательного звена

В данном случае звено нельзя разбить на более простые звенья, и его надо рассматривать как единое целое (3.20).

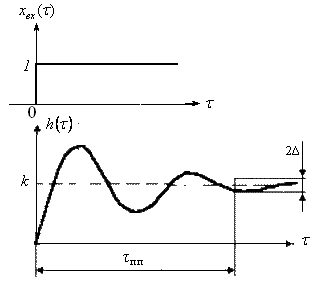
Рисунок – Переходная характеристика колебательного звена

Определим импульсную переходную функцию колебательного звена. Для этого необходимо решить уравнение (3.37) при единичном импульсном изменении входной координаты (3.7):

Решение имеет вид:

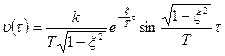(3.46)

График импульсной переходной функции приведен на рисунке (3.21).

Определим частотные характеристики колебательного звена, подставив jω вместо р в передаточную функцию (3.38):

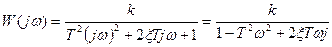(3.47)

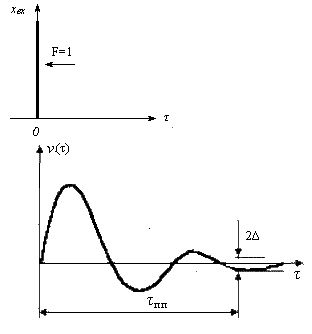
Рисунок – Импульсная переходная функция колебательного звена

Освободившись от иррациональности в знаменателе, получим

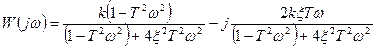(3.48)

Из выражения (3.48) получим АЧХ и ФЧХ.

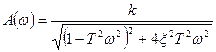(3.49)

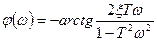(3.50)

АФХ в показательной форме имеет вид:

(3.51)

Графики АЧХ, ФЧХ и АФХ приведены на рисунках 3.22, 3.23 и 3.24.

Примеры колебательного звена приведены на рисунке 3.25.

Рисунок 3.25 – Примеры колебательных звеньев

Дата добавления: 2014-01-11