Последовательное соединение звеньев

Соединение звеньев

Если имеются уравнения всех звеньев системы, то описанием последней является система этих уравнений. Исключая из нее промежуточные переменные, можно получить одно дифференциальное уравнение высокого порядка, связывающее выходную величину системы с определенной входной величиной – каким-либо возмущением или задающим воздействием. Однако значительно более просто можно получить описание системы, если оперировать передаточными функциями звеньев. При этом в системах любой сложности можно выделить только три типа соединения звеньев: последовательное, параллельное и встречно-параллельное соединение.

Последовательным называют такое соединение, при котором выходная координата предыдущего звена является входной координатой последующего звена (рис 4.1)

Рисунок 4.1 - Последовательное соединение звеньев

Для данного соединения запишем известные соотношения.

(4.1)

(4.2)

(4.3)

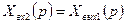
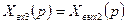
(4.4)

Перемножая левые и правые части уравнений (4.1)-(4.3), получим:

(4.5)

Учитывая равенство (4.4), получим

(4.6)

Таким образом, передаточная функция последовательно соединенных звеньев равна произведению передаточных функций звеньев, входящих в это соединение.

(4.7)

В качестве примера можно привести реальное интегрирующее звено с передаточной функцией 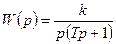, которое эквивалентно последовательному соединению звеньев идеального интегрирующего с передаточной функцией и инерционного звена первого порядка с передаточной функцией .

Дата добавления: 2014-01-11