Аналитические методы исследования объектов управления

При аналитическом методе получения математического описания объектов управления необходимо достаточно полно изучить конструкцию агрегата, технологический процесс, протекающий в этом агрегате, Характер и направление протекания процессов соответствуют тем или иным физическим законам, математическая формулировка которых и определяет уравнение, которое может быть положено в основу анализа объекта. Как правило, в объектах управления протекают процессы массо- и теплопереноса, описание которых может быть получено с помощью дифференциальных уравнений. Однако в этом случае приходится прибегать к некоторым упрощениям. В частности, поскольку реальные объекты управления являются нелинейными, то в первую очередь следует линеаризовать нелинейные зависимости путем разложения заданных функций в ряд Тейлора. Кроме того, представляя объект как некоторую совокупность типовых элементарных звеньев, будут получены уравнения невысокой точности. Поэтому к этому методу прибегают при отсутствии самого объекта, т.е. на стадии его проектирования.

Рассмотрим пример составления дифференциального уравнения для астатического объекта управления, т.е. объекта без самовыравнивания (рис. 5.4).

Рисунок 5.4 – Астатический объект управления

1 – объект управления; 2 – насос.

Для составления дифференциального уравнения воспользуемся материальным балансом. В состоянии равновесия клапан на трубопроводе подачи жидкости на входе открыт на определенную величину, при которой расход жидкости составляет Q _пр, и в этом случае имеет место равенство:

Q _пр =Q _ст (5.3)

Величина притока жидкости определяется степенью открытия клапана:

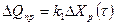(5.4)

Изменение расхода жидкости на притоке вызовет изменение уровня жидкости в ёмкости

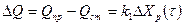(5.5)

Это приведет к изменению уровня жидкости в ёмкости:

(5.6),

где S – площадь поверхности жидкости в ёмкости.

С другой стороны

(5.7)

Приравнивая правые чести уравнений (5.6) и (5.7), получим

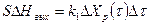(5.8)

Из уравнения (5.8) окончательно получим:

(5.9)

Уравнение (5.9) очень часто записывают в виде:

(5.10)

Найдем изменение выходной координаты при скачкообразном изменении входной координаты

(5.11)

Изобразим графически процессы, протекающие в объекте управления (рис. 5.5)

Рисунок 5.5 – Кривая разгона объекта управления и изменения притока и стока

Объект управления, у которого реакция на скачкообразное воздействие представляет собой скорость изменения выходной координаты, пропорциональную возмущению, и выходная координата не приходит к новому установившемуся значению называют астатическими объектами или объектами без самовыравнивания.

Рассмотрим пример составления дифференциального уравнения для статического объекта с самовыравниванием (рис. 5.6).

Рисунок 5.6 - Статический объект с самовыравниванием

Задача заключается в отыскании уравнения, связывающего выходную координату и входную координату . Запишем начальные условия

(5.12)

Переместим регулирующий орган на величину

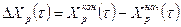(5.13)

Или

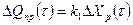(5.14)

Расход жидкости на выходе ёмкости определяется равенством

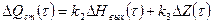(5.15)

При ΔZ(τ)=0 получим

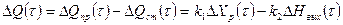(5.16)

Изменение объёма жидкости в ёмкости можно определить по формулам:

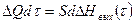(5.17)

(5.18)

Из уравнения (5.18) получим

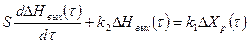(5.19)

Переходя к пределу и обозначая

(5.20),

получим

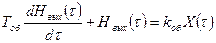(5.21)

При скачкообразном изменении входной координаты получим кривую разгона

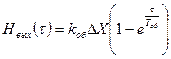(5.22)

Характер изменение выходной и входной координат приведен на рисунке 5.7. У данного объекта выходная координата при скачкообразном изменении входной координаты стремится к новому установившемуся значению. Объекты управления, у которых выходная

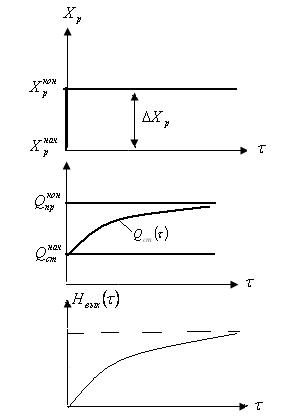
Рисунок 5.7 – Кривая разгона статического объекта и изменение притока и стока

координата при скачкообразном изменении входной координаты стремится к новому установившемуся значению называются статическими. Статические объекты в практике автоматизации производственных процессов встречаются чаще, чем астатические. Управление статическими объектами проще, чем астатическими.

Дата добавления: 2014-01-11