Обработка кривой разгона статического объекта

По экспериментальным данным строим кривую разгона статического объекта (рис. 5.16).

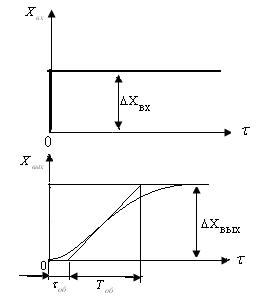
Рисунок 5.16 – Кривая разгона статического объекта

Выбор передаточной функции осуществим из следующих соображений. Предположим, что ступенчатое возмущающее воздействие было подано на вход запаздывающего звена, а его выходная координата поступает на вход апериодического звена. Характер переходных процессов, происходящих в этом случае, представлен на рисунке 5.17. В соответствии с рисунком 5.17 реальный объект можно представить как последовательное соединение запаздывающего и апериодического звеньев (рис. 5.18).

Так как передаточная функция апериодического звена имеет вид:

а запаздывающего -

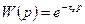
Рисунок 5.17 - К определению вида передаточной функции статического объекта

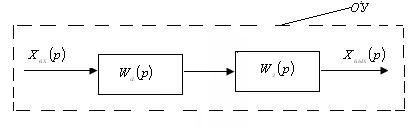
Рисунок 5.18 - Структурная схема статического объекта

то передаточная функция объекта управления имеет вид:

(5.30)

Параметры передаточной функции определяем из графика кривой разгона (рис. 5.16).

(5.31)

Для определения постоянной времени и времени запаздывания необходимо провести касательную к кривой разгона в точке наибольшей скорости изменения выходной координаты (в точке перегиба кривой). Отрезок, который отсекает касательная на оси времени и будет соответствовать времени запаздывания, проекция отрезка касательной, заключенного между старым и новым установившимися значениями, на ось времени определяет постоянную времени.

Физический смысл параметров статического объекта следующий:

τ_об – характеризует отставание реакции объекта на возмущающее воздействие;

Т_об – характеризует инерционность объекта, быстроту протекания процессов; чем больше постоянная времени, тем медленнее протекает переходный процесс;

К_об – характеризует усилительные свойства объекта в статическом режиме.

По величине Т_об объекты подразделяют на:

а) инерционные объекты, у которых постоянная времени больше 20 секунд (к ним относят объекты с регулируемыми координатами температуры, газового состава, влажности, солесодержания);

б) малоинерционные объекты, у которых постоянная времени меньше 10 секунд (к ним относят объекты с регулируемыми координатами расхода, уровня, соотношения расходов топлива и воздуха).

Определение параметров передаточной функции статического объекта можно осуществить и методом двух координат. Метод двух координат является эмпирическим методом и суть его заключается в следующем. Коэффициент передачи объекта определяется также, как и в предыдущем случае. Для определения постоянной времени и времени запаздывания на кривой разгона выбирают две точки (рис. 5.19).

Рисунок 5.19 – Определение параметров объекта методом двух координат

Положение точек на кривой разгона определяют следующим образом:

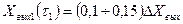(5.32)

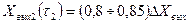(5.33)

Приведенные координаты (5.32) и (5.33) приводят к безразмерному виду:

(5.34)

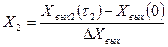(5.35)

Для определения времени запаздывания и постоянной времени пользуются эмпирическими формулами:

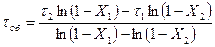(5.36)

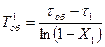(5.37)

или

(5.38)

Объект управления с полученными параметрами можно рассматривать как последовательное соединение запаздывающего и апериодического звеньев. Однако такая модель объекта не абсолютно адекватна реальному объекту. Поэтому в некоторых случаях прибегают к трехзвенной аппроксимации, представляя объект управления как последовательное соединение трех звеньев: двух апериодических звеньев и звена чистого запаздывания (рис. 5.20). Передаточные функции указанных звеньев имеют вид:

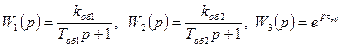
В этом случае передаточная функция объекта имеет вид:

Рисунок 5.20 – Трехзвенная аппроксимация объекта управления

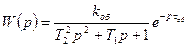(5.39)

(5.40)

Дата добавления: 2014-01-11