Передаточные функции разомкнутой и замкнутой системы управления

Линейные системы автоматического управления

АСУ представляет собой динамически взаимодействующую, упорядоченную совокупность объекта управления и регулятора.

Обобщенная структурная схема АСУ имеет вид (рис. 7.1):

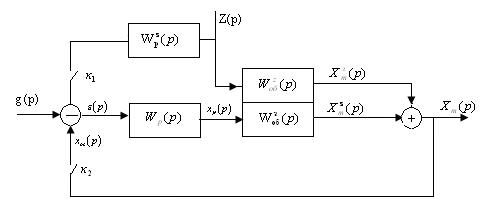
Рисунок 7.1 – Структурная схема АСУ

Выходной координатой системы является текущее значение. При этом выходная координата системы совпадает с выходной координатой объекта. В АСУ есть две точки приложения возмущающих воздействий: одна точка, где человек изменяя задание, вносит возмущающее воздействие по заданию; вторая точка, где возмущающие воздействия не зависят от воли человека и поступают непосредственно на вход объекта.

Например, в печи при заданной температуре 1200 ⁰С непрерывно нагревают заготовки, поступающие в печь с температурой 600 ⁰С. Если необходимо изменить температуру нагрева заготовок, оператор устанавливает новое заданное значение регулируемой координаты, т.е. вносит возмущение по заданию. Но может быть ситуация, когда не надо изменять задание, а непредвиденно в печь начинают поступать заготовки с температурой равной нулю. Естественно, что температура в печи начнет снижаться, а регулятор будет стремиться вернуть её к заданному значению. Таким образом при установившемся состоянии g(τ), Z(τ) и Х_m(τ) имеют определенное постоянное значение. При изменении g(τ) или Z(τ), т.е. при отклонении этих величин от установившегося состояния, в системе начинает протекать переходный процесс. Если известно, как изменяются g(τ) или Z(τ), то для того чтобы определить, как протекает переходный процесс в системе, необходимо знать передаточные функции по каналу возмущающего воздействия.

В зависимости от положения ключей (рис. 7.1) будем иметь разные типы систем.

Вариант 1. Ключ к₁ и ключ к₂ разомкнуты. В этом случае представленная система является разомкнутой, регулятор не реагирует на возмущение по нагрузке, а объект реагирует.

Вариант 2. Ключ к₁ замкнут, а ключ к₂ разомкнут. В этом случае представленная система также является разомкнутой, которая работает, используя принцип управления по возмущению.

Вариант 3. Ключ к₁ разомкнут, а ключ к₂ замкнут. В этом случае представленная система является замкнутой, которая работает, используя принцип управления по отклонению.

Вариант 4. Ключ к₁ замкнут, а ключ к₂ замкнут. В этом случае представленная система является комбинированной, которая работает, используя принцип управления по возмущению и по отклонению.

Цель функционирования системы – поддержание текущего значения регулируемого параметра на заданном уровне. В случае, когда на АСУ действует только возмущение по нагрузке, то цель функционирования системы заключается в подавлении возмущающего воздействия. При 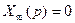имеет место идеальное подавление возмущения по нагрузке.

Когда на систему воздействует возмущение по заданию, то целью функционирования системы является воспроизведение заданного значения параметра. При идеальном воспроизведении должно соблюдаться равенство .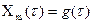

Определим зависимость между выходной и входной координатами системы, а также передаточные функции при условии, что на систему одновременно действуют возмущения по нагрузке и по заданию.

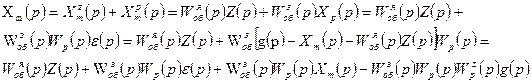(7.2)

Уравнение (7.2) перепишем в следующем виде:

(7.3)

Из уравнения (7.3) определим текущее значение регулируемой координаты:

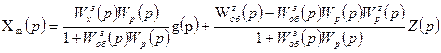(7.4)

Из уравнения (7.4) определим передаточную функцию замкнутой системы относительно возмущающего воздействия по заданию. В этом случае Z(p)=0.

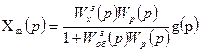(7.5)

Откуда

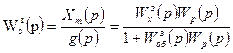(7.6)

В случае когда заданное значение регулируемой координаты не изменяется, т.е. Х_з(р)=0, и используется принцип управления по нагрузке, получим:

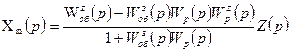(7.7)

Из уравнения (7.7) получим передаточную функцию по каналу нагрузки:

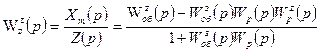(7.8)

Если АСУ разомкнута, т.е. ключ к₂ разомкнут, то получим передаточную функцию разомкнутой системы:

(7.9)

Идеальное воспроизведение задания возможно только в том случае, когда выполняется условие

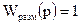(7.10)

Используя уравнение (7.9), условие идеального воспроизведения можно записать следующим образом:

(7.11)

В реальных условиях уравнение (7.11) выполнить невозможно, поэтому системы с идеальным воспроизведением не существуют. Например, если передаточная функция объекта

имеет вид: , то построить регулятор с передаточной функцией 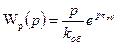невозможно.

Если на систему действует возмущение по нагрузке, то передаточная функция разомкнутой системы запишется следующим образом:

(7.12)

Идеальное подавления возмущения по нагрузке наблюдается тогда, когда 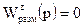, или 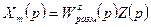. Системы, для которых выполняются эти условия, называются инвариантными.

Определим передаточную функцию устройства ввода возмущения, обеспечивающего инвариантность системы. Для этого приравняем правую часть уравнения (7.12) к нулю. Из полученного равенства будем иметь:

(7.13)

Если ключи к₁ и к₂ разомкнуты, то система не реагирует на возмущения по нагрузке, а её передаточная функция определяется уравнением (7.9).

Если ключ к₁ разомкнут и ключ к₂ замкнут, то система работает, используя принцип управления по отклонению, для которой справедливо равенство:

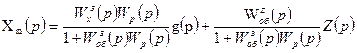(7.14)

Из равенства (7.14) получим передаточную функцию по каналу задающего воздействия (передаточная функция воспроизведения):

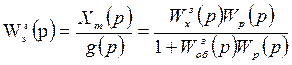(7.15)

И передаточную функцию по каналу нагрузки (передаточная функция подавления):

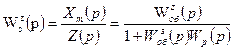(7.16)

В частном случае, когда

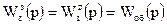
получим

(7.17)

Дата добавления: 2014-01-11