Критерий устойчивости Гурвица

Критерии устойчивости

Определение устойчивости АСУ по корням характеристического уравнения сопряжено с большими трудностями, связанными с решением дифференциального уравнения и большим объемом вычислений. Поэтому в практике ТАУ для определения устойчивости чаще используют критерии устойчивости.

Критерием устойчивости называется совокупность правил, методов или алгоритмов, которые позволяют судить об устойчивости АСУ без решения характеристического уравнения, используя другие признаки. Все критерии можно разделить на две группы: алгебраические критерии устойчивости и частотные критерии устойчивости. К алгебраическим критериям устойчивости относятся:

1) критерий устойчивости Вишнеградского;

2) критерий устойчивости Гурвица;

3) критерий устойчивости Рауса.

. К частотным критериям устойчивости относятся:

4) частотный критерий устойчивости Найквиста;

5) частотный критерий устойчивости Михайлова.

Критерий устойчивости Гурвица можно сформулировать в форме, предложенной автором:

Если система описывается линейным дифференциальным уравнением, характеристическое уравнение которого имеет вид:

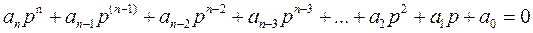(8.5)

то для того, чтобы она была устойчива, т.е. чтобы все действительные корни и действительные части комплексных корней характеристического уравнения были бы отрицательны, необходимо и достаточно, чтобы все коэффициенты уравнения имели бы один и тот же знак, а диагональный детерминант порядка п-1, составленный из коэффициентов уравнения, и все его диагональные миноры были бы положительными.

Диагональный детерминант составляется следующим образом: по диагонали определителя выписывают коэффициенты характеристического уравнения, начиная с a_n-1 по а₁. Таким образом, получается матрица, содержащая n-1 строку и n-1 столбец. Столбцы заполняют следующим образом: вверх выписывают коэффициенты с убывающими индексами, а вниз – с возрастающими. При достижении нулевого или n -го индекса далее ставят нули.

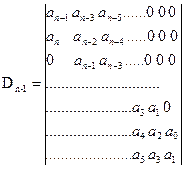(8.6)

Таким образом, получается квадратная матрица размером (n-1) * (n-1), на главной диагонали которой расположены коэффициенты от a_n-1 по a₁.

Каждый диагональный минор получают из предыдущего минора путем вычеркивания последней строки и последнего столбца.

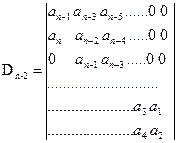(8.7)

(8.8)

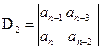(8.9)

D₁=a_n-1 (8.10)

Для решения вопроса об устойчивости АСУ выполняется анализ матрицы по следующим правилам:

1) если определители матрицы и всех диагональных миноров положительны, то АСУ устойчива;

2) если определитель или хотя бы один минор равен нулю, то АСУ находится на границе устойчивости;

3) если определитель или хотя бы один минор отрицательны, то АСУ неустойчива.

Рассмотрим конкретные примеры исследования систем на устойчивость с помощью критерия Гурвица.

Пример №1. АСУ включает статический объект второго порядка с передаточной функцией 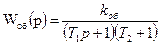и интегральный регулятор с передаточной функцией 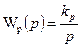. Определить при каком значении коэффициента передачи регулятора система будет устойчивой.

Запишем передаточную функцию замкнутой системы, при этом неважно по какому каналу будет записана передаточная функция, так как нас будет интересовать только знаменатель передаточной функции.

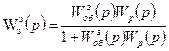(811)

Знаменатель передаточной функции, приравненный к нулю, является характеристическим уравнением, т.е.

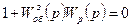(8.12)

Подставим в уравнение (8.12) значения передаточных функций:

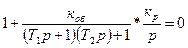(8.13)

Приводя уравнение (8.13) к общему знаменателю и приравнивая числитель к нулю, получим характеристическое уравнение для системы

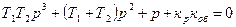(8.14)

Составим главный детерминант, который для данного случая имеет второй порядок:

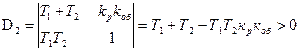(8,15)

Из последнего равенства получим

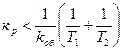(8.16)

В уравнении (8.16) слева записан параметр настройки регулятора, а справа параметры объекта. Чтобы система была более устойчивой, необходимо иметь как можно меньшее значение коэффициента передачи регулятора. Но в этом случае регулятор будет медленно воздействовать на объект. Поэтому приходится принимать компромиссное решение: чтобы система была устойчивой и регулятор достаточно быстро воздействовал на объект.

Если в уравнении (8.16) поставить знак равенства, т.е. , то система окажется на границе устойчивости. Если 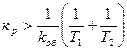, то система будет неустойчивой. Поскольку параметры объекта изменяются довольно медленно, то воздействовать на характер переходного процесса можно, изменяя параметры регулятора.

Коэффициент передачи регулятора, при котором система оказывается на границе устойчивости, называется критическим.

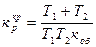(8.17)

Условие (8.17) можно записать и так

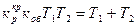(8.18)

Уравнение (8.18) перепишем в форме

XY=1 (8.19)

Уравнение (8.19) является уравнением гиперболы Вышнеградского, который сформулировал критерий устойчивости для систем, описываемых уравнениями не выше третьего порядка.

При переходе от уравнения (8.18) к уравнению (8.19) необходимо соблюдать следующие правила:

1) параметры X и Y должны быть безразмерными;

2) параметр X должен быть пропорционален коэффициенту передачи регулятора.

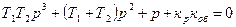
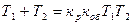
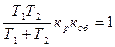
(8.20)

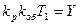(8.21)

Построим гиперболу Вышнеградского в полученных координатах (рис. 8.4).

Рисунок 8.4 – Гипербола Вышнеградского для систем третьего порядка

Пример №2. Рассмотрим задачу, сформулированную в примере №1, но для случая, когда объект имеет передаточную функцию вида

Приравняв в уравнении (8.14) Т₂ к нулю, получим характеристическое уравнение

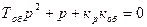(8.22)

Составим главный детерминант, который для данного случая имеет первый порядок:

D₁=1>0

Получено условие, которое выполняется при любых параметрах системы.

Системы, которые при определенных значениях своих параметров могут быть устойчивыми, называются структурно-устойчивыми.

Пример №3. АСУ включает астатический объект второго порядка с передаточной функцией 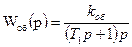и интегральный регулятор с передаточной функцией 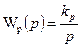. Определить, при каком значении коэффициента передачи регулятора система будет устойчивой.

Используя уравнение (8.13) и подставляя в него значения передаточных функций, получим

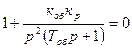(8.23)

или

(8.24)

Перепишем уравнение (8.24) следующим образом:

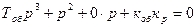
Тогда главный детерминант примет вид:

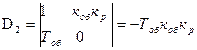
В данном случае главный детерминант отрицательный, т.е. система неустойчивая, при этом она неустойчивая при любых своих параметрах. О таких системах говорят, что она структурно-неустойчивая.

Из последнего примера можно сделать вывод: что интегральный регулятор нельзя устанавливать на астатическом объекте, так как в любом случае мы получим неустойчивую систему.

Несмотря на простоту применения критерия Гурвица, он обладает рядом недостатков:

1) необходимо рассматривать передаточную функцию замкнутой системы, которая получается достаточно сложной;

2) с помощью критерия можно анализировать системы, у которых в знаменателе передаточной функции стоит рациональный многочлен.

Действительно, если передаточная функция объекта 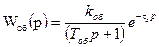, а регулятора 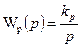, то характеристическое уравнение имеет вид:

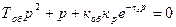(8.25)

С помощью критерия устойчивости Гурвица эту систему исследовать нельзя. В этом случае нужны другие критерии.

Дата добавления: 2014-01-11