Критерий устойчивости Найквиста. Этот критерий, предложенный в 1932 году американским ученым Найквистом, позволяет судить об устойчивости замкнутой линейной системы регулирования по виду

Этот критерий, предложенный в 1932 году американским ученым Найквистом, позволяет судить об устойчивости замкнутой линейной системы регулирования по виду амплитудно-фазовой характеристики той же системы в разомкнутом состоянии. Критерий устойчивости Найквиста является более универсальным, так как позволяет оценивать устойчивость замкнутых автоматических систем (рис. 8.5) как обладающих запаздыванием, так и систем без запаздывания.

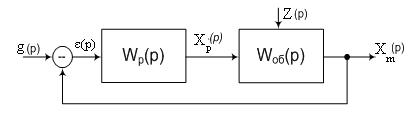
Рисунок 8.5 – Структурная схема системы автоматического управления

Передаточная функция замкнутой АСУ по каналу задания имеет вид:

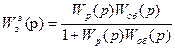(8.26)

Знаменатель в (8.26) является характеристическим уравнением АСУ:

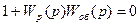(8.27)

Последнее выражение можно переписать так

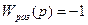(8.28)

АСУ будет находиться на границе устойчивости, если её характеристическое уравнение содержит пару чисто мнимых корней. Потребовать наличие чисто мнимых корней можно подстановкой p=jω в характеристическое уравнение.

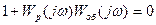(8.29)

На основании выражения (8.29) получим критерий устойчивости Найквиста.

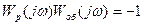(8.30)

Для геометрической интерпретации решения вопроса об устойчивости замкнутой системы управления необходимо построить АФХ разомкнутой системы. Поскольку АФХ объекта имеет вид:

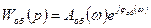(8.31)

а АФХ регулятора –

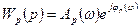(8.32)

То для соблюдения равенства (8.30) необходимо, чтобы

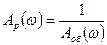(8.33)

и

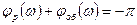(8.34)

Таким образом, точка с координатами (- 1; j0) и является той точкой, при прохождении через которую годографа АФХ разомкнутой системы сама система оказывается на границе устойчивости. На рисунке 8.6 такой кривой является кривая 1. Для кривой 2 это условие не выполняется, и замкнутая система управления будет устойчивой. В этом случае говорят, что АФХ разомкнутой системы не охватывает точку с координатами (- 1; j0). Для кривой 3 это условие также не выполняется, но в этом случае замкнутая система управления будет неустойчивой. В этом случае говорят, что АФХ разомкнутой системы охватывает точку с координатами (- 1; j0).

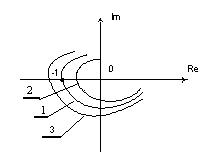
Рисунок 8.6 – Геометрическая интерпретация критерия устойчивости Найквиста

Рассмотрим физическую интерпретацию критерия устойчивости Найквиста.

Рисунок 8.7 – К вопросу физической интерпретации критерия устойчивости Найквиста

Предположим, что проводим эксперимент по снятию частотных характеристик разомкнутой системы. При этом ключ к₁ замкнут, а ключ к₂ разомкнут и на вход системы подается синусоидальное воздействие

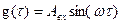(8.35)

Частоту колебаний можно изменять, и при определенной частоте получим, что сдвиг фаз составляет π, т.е.

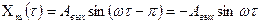(8.36)

В этом состоянии разомкнем ключ к₁ и замкнем ключ к₂. Или, другими словами, мысленно прекратив подачу входных колебаний и замкнув систему обратной связью, что выходные колебания заменять собою входные колебания. При этом можно наблюдать три случая:

1) 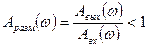(8.37)

это говорит о том, что колебания в системе со временем будут затухать, т.е. система будет устойчивой;

2) 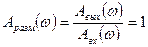(8.38)

это говорит о том, что колебания в системе будут незатухающими, т.е. система будет на границе устойчивости;

3) 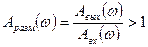(8.39)

это говорит о том, что колебания в системе будут расходящимися, т.е. система будет неустойчивой;

Дата добавления: 2014-01-11