Запас устойчивости по модулю и фазе

Рассмотрим на комплексной плоскости годограф АФХ разомкнутой системы, соответствующий устойчивой замкнутой системе (рис. 8.8).

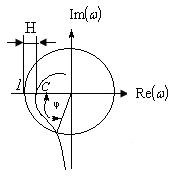
Рисунок 8.8 – Определение запаса устойчивости по модулю и фазе

На этой же плоскости проведем окружность радиусом, равным единице, и точку пересечения АФХ разомкнутой системы и окружности соединим с началом координат. Запас устойчивости можно оценить двумя показателями: это расстояние точки с координатами (-1; 0j) до точки С, определяемой величиной Н, и угол φ, на который необходимо повернуть дополнительно модуль АФХ, чтобы система вышла на границу устойчивости. Запасы устойчивости по модулю и фазе характеризуют степень удаления АФХ разомкнутой системы от границы устойчивости. Чем больше Н и φ, тем дальше система удалена от опасной точки (-1; 0j).

При к_р=0, что соответствует отсутствию регулятора, Н=1, запас устойчивости по модулю в этом случае не определен. Если Н=0 и φ=0, то замкнутая система управления находится на границе устойчивости.

Запас устойчивости по модулю Н показывает, на сколько можно увеличить модуль АФХ разомкнутой системы при φ_разм (ω)=-π, чтобы замкнутая система вышла на границу устойчивости.

Запас устойчивости по фазе показывает, на сколько можно увеличить сдвиг по фазе разомкнутой системы, чтобы замкнутая система вышла на границу устойчивости.

Если φ(ω)<0 или Н<0, то замкнутая система неустойчивая.

Рассмотрим конкретный пример. АСУ состоит из объекта управления с передаточной функцией 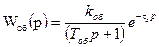и идеального пропорционального регулятора с передаточной функцией .

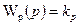Определить устойчивость замкнутой системы, если к_об=1⁰С/%ХРО, Т_об=100 с, τ_об=100 с, к_р=2 %ХРО/⁰С. Если АСУ устойчивая, то определить запас устойчивости по модулю и фазе.

Решение. Запишем передаточную функцию разомкнутой системы:

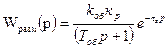
Заменяя в передаточной функции р на jω, получим АФХ разомкнутой системы:

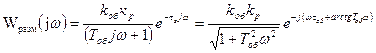
Определим частоту, при которой модуль АФХ разомкнутой системы равен 1.

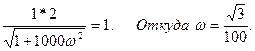Подставляя ω в выражение ФЧХ, получим

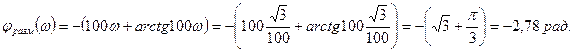
Тогда запас устойчивости по фазе составит

φ=3,14-2,78=0,36 рад.

Таким образом, исследуемая система является устойчивой и обладает запасом устойчивости по фазе, равным 0,36 радиан.

Запас устойчивости по модулю определим, найдя частоту, при которой АФХ разомкнутой системы пересекает отрицательную действительную полуось. Эта частота равна ω=2,326 1/с. При этом А(2,326)=0,86. Запас устойчивости по модулю равен 0,14.

Дата добавления: 2014-01-11