Основные понятия и определения. 1. Информатика: Учебное пособие для среднего профессионального образования / Под общ

Л.1 ДВОЙНОЙ ИНТЕГРАЛ В ДЕКАТОВЫХ КООРДИНАТАХ.

Дополнительная

Основная

1. Информатика: Учебное пособие для среднего профессионального образования / Под общ. ред. И.А. Черноскутовой. – СПб.: Питер, 2005. – 272 с.

2. Информатика. Базовый курс / Под ред. С.В. Симоновича. – СПБ.: Питер, 2006. – 639 с.

3. Макарова Н.В. Информатика: Учебник. – М.: Финансы и статистика, 2007. – 786 с.

4. Михеева Е.В. Практикум по информатике: Учеб. пособие для сред. проф. образования. – 2-е изд., стер. – М.: Издательский центр «Академия», 2004. – 192 с.

1. Безручко В.Т. Практикум по курсу «Информатика». Работа в Windows, Word, Excel: Учеб. пособие. – М.: Финансы и статистика, 2002. – 272 с.

2. Информатика для ссузов: Учебное пособие / П.П. Беленький и др.; Под общ. ред. П.П. Беленького. – М.: КНОРУС, 2005. – 448 с.

3. Угринович Н.Д. Информатика и информационные технологии: Учебник для 10-11 классов. – 2-е изд. – М.:
БИНОМ: Лаборатория знаний, 2005. – 511 с.

Рассмотрим на плоскости ХОУ замкнутую область Д, т.е. такую область, которая ограничена замкнутой линией Г границей области, причем точки лежащие на границе принадлежат Д.

Пусть функция z=f(x,y) непрерывна в области Д.

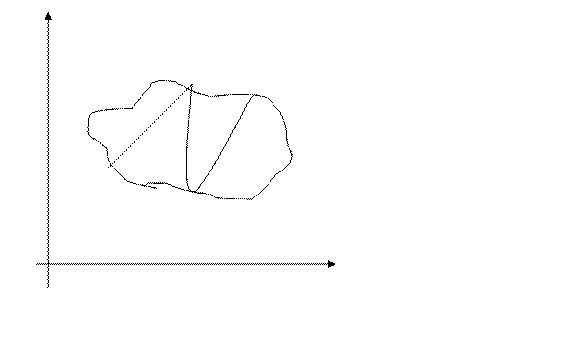
1. Разобьем область Д произвольным образом на n-равных областей (площадок) Д_i (i=1,n), площади которых обозначим через ∆Si. Наибольшее расстояние между двумя точками каждой площадки назовем диаметром площадки. А наибольший среди них – диаметром разбиения области Д.

λ=max{λi}

2.Выберем на каждой площадке Дi произвольную точку Mi(Xi,Yi), умножим значение функции в этой точке f(Xi,Yi) на ∆Si и составим сумму всех таких произведений.

f(X1,Y2)* ∆S1+ f(X2,Y2)* ∆S2+……+f(Xn,Yn)* ∆Sn= (1)

Опр.1 сумма (1) наз. интегральной суммой для функции f(X,Y) в области Д.

Опр.2 если существует конечный предел интегральной суммы (1) при n->∞,так что диаметр разбиения λ->0, то он называется двойным интегралом от функции f(x,y) по области Д и обозначается:

где

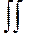-символ двойного интеграла

Д-область интегрирования

f(x,y)-подынтегральная функция

х,у – переменные интегрирования

ds –элемент площади

Таким образом

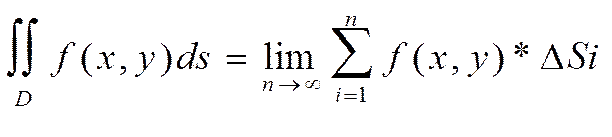
Теорема1: (Достаточное условие существования двойного интеграла) если функция z=f(x,y) непрерывна в рассматриваемой области Д, то существует конечный предел интегральной суммы (1) (т.е. ДВИ) и этот предел не зависит от способа разбиения области Д на площадки Дi и от выбора точек на них для составления интегральной суммы.

Из теоремы 1 следует, что разбиение области Д на площадки можно осуществить самым простым способом – линиями параллельными координатным осям.

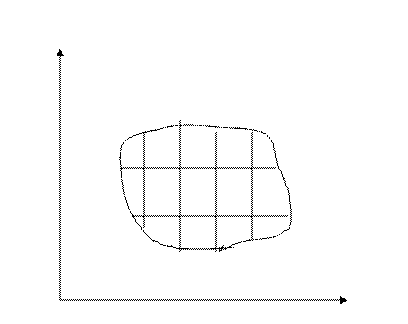
Тогда площадка Дi-прямоугольник, со сторонами ∆Х, ∆У. ∆S=∆x*∆y,т.к. для независимых переменных х и у, ∆х=dx, ∆y=dy.

Ds=∆S=∆x*∆y=dx*dy.

Дата добавления: 2014-01-11