Основные понятия и определения КРИ-II, теорема существования

КРИ является обобщением понятия ОИ на случай, когда область интегрирования – не отрезок оси ОХ или ОУ, а дуга кривой на плоскости или в пространстве.

Пусть на плоскости ХОУ задана непрерывная кривая L и функция P(x,y), которая определена во всех точках дуги АВ этой кривой L.

- Разобьем дугу АВ в направлении от А до В произвольным образом n частичных дуг с длинами .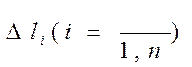

Обозначим через наибольшую из длин всех частичных дуг, т.е. 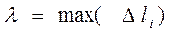, которую называют диаметром разбиения дуги АВ на части.

- Выберем на каждой частичной дуге произвольную точку 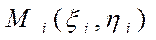и составим сумму:

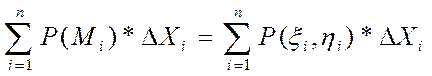(1)

Где ()- проекции частичных дуг на ось ОХ.

Сумма (1) наз. интегральной суммой для функции P(x,y) по переменной х.

Опр.1: если сущ. конечный предел интегральной суммы (1), когда 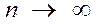(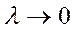), то он наз. криволинейным интегралом по переменной (по координате) х от функции P(x,y) по дуге (по кривой) АВ в направлении от А до В и обозначается:

Таким образом:

(2)

Где АВ – путь интегрирования (А), (В)- пределы интегрирования, P(x,y)- подынтегральная функция, х – переменная интегрирования.

Аналогично можно ввести КРИ по переменной у от функции Q(x,y):

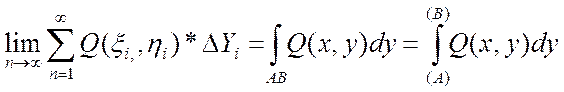(3)

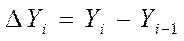
Где (), где 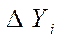- проекции частичных дуг на ось ОУ.

Опр.2: Сумма интегралов и наз. КРИ по координатам общего вида или КРИ-II, т.е. 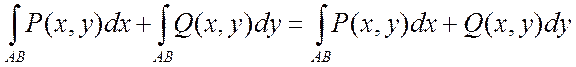(4)

Опр.3 Если начальная и конечная точки дуги АВ совпадают, т.е. АВ- замкнутый контур Г, который не пересекает сам себя, то такие КРИ наз. КРИ по замкнутому контуру или контурными интегралами и обозначаются:

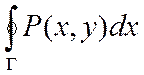
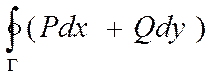
Для обхода по замкнутому контуру сущ. 2 возможных варианта по часовой стрелке и против.

Опр.4 Направление обхода замкнутого контура считается положительным (отрицательным), если он осуществляется против (по) часовой стрелке, т.е. так что при обходе по контуру область ограниченная этим контуром остается слева (справа).

При положительном направлении обхода в символе КРИ опускают

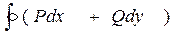
Пусть дуга АВ ил и замкнутый контур Г заданы в параметрической форме, м.е. с помощью двух уравнений x=x(t), y=y(t), где

Теорема 5.1. (О существовании КРИ-II):

1) функции x(t), y(t) непрерывно дифференцируемы на отрезке , т.е. АВ- гладкая кривая

2) функции P(x(t),y(t)) и Q(x(t),y(t)) как функции t непрерывны на , то КРИ –II сущ., т.е. существуют конечные пределы интегральных сумм и они не зависят от способа разбиения дуги АВ на части и от выбора точек на них для составления интегральных сумм.

Если АВ - пространственная кривая в точках которой определены функции трех переменных P(x,y,z) Q(x,y,z) R(x,y,z) то все изложенное можно обозначить:

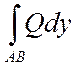
Дата добавления: 2014-01-11