Условия независимости КРИ 2-го рода от формы пути интегрирования (продолжение)

КРИ независящая от формы пути интегрирования обозначается следующим отрезком.

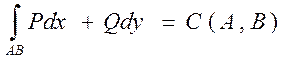
Е(А,В) – значение КРИ, который зависит только от расположения точек А и В.

Теорема 7.1. (необходимое и достаточное условие независимости КРИ от формы пути интегрирования).

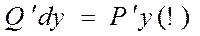
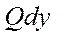Для того чтоб КРИ 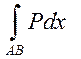и в обл. D не зависит от формы пути интегрирования необходим и достаточно чтоб, в каждой т. Обл. D выполнялось условие т.е.

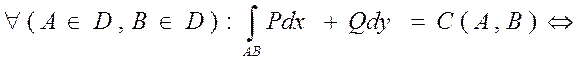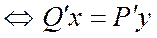
Докажем достаточность этой теоремы:

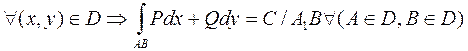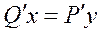Рассмотрим в обл. D производную замкнутый контур Г, проходящий через т. А и В, запишем этого контура формулу Грина:

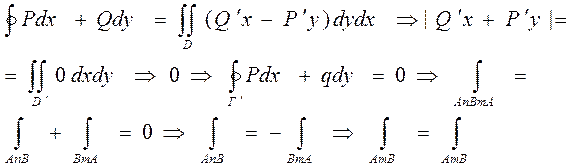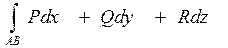Последнее равенство и означает, что КРИ не зависит от формы пути интегрирования, что и т.д.

Для пространственного интеграла,

где АВ – пространственная кривая во всех точках от функции 3-х переменных интегрирования вместе со своим ЧП P=P(x,y,z) Q=Q(x,y,z), R=R(x,y,z), условие независимости КРИ:

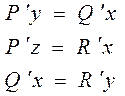Из теоремы ф-ции нескольких переменных известно, что полный дифференциал (ПД) ф-ции U=U(x,y) имеет вид:

Теорема 7.2 (критерий полного дифференциала)

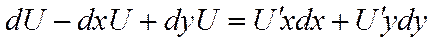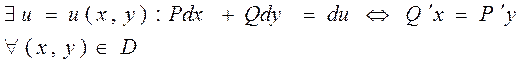
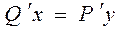Выражение Pdx+Qdy в обл. D представляет собой выражение Pdx+Qdy ПД некоторой ф-ции U=U(x,y) тогда, когда во всех точках обл. D выполняется условие

И

Докажем необходимость ()

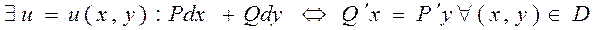По определению du=U’xdx+U’ydy

по условию du=Pdx+Qdy.

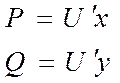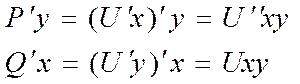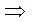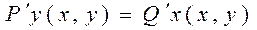Т. к. по условию теоремы непрерывно то будет непрерывны и Uxy и U’’yx, тогда по теореме смежных производных имеем: U’’xy-U’’yx=P’y=P’x

Теорема 7.3 (условие независимых КРИ 2-го рода от формы пути интегрирования на языке полного дифференциала)

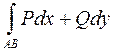Для того чтоб КРИ по функции не зависел от формы пути интегрирования в обл. D, в которой ф-ции P(x,y) и Q(x,y) непрерывны вместе со своими ЧП, необходимо и достаточно чтоб в каждой т. этой обл. выражение Pdx+Qdy являлось D некоторой функции U=U(x,y)

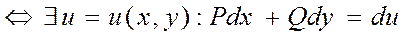Док-во:

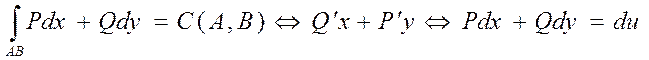Покажем что если КРИ не зависит от формы пути интегрирования, который соединяет точки А и В то его значения равно разности знач. ф-ции U=U(x,y) в т. В и в т. А для которых выражение Pdx и Qdy есть полным дифференциалом т.е.:

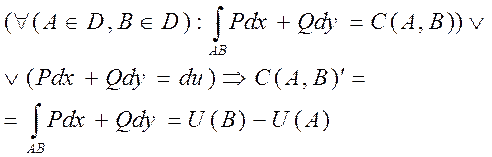(4)

Формула (4) обобщённая формула Ньютона-Лейбница для КРИ от полного дифференциала. Док-во:

=

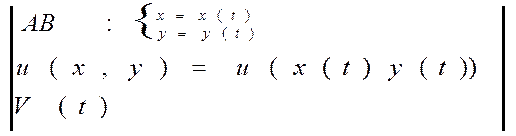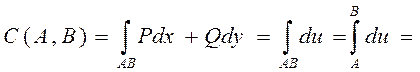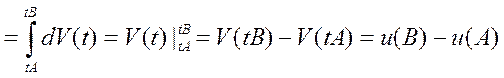Чтобы найти ф-цию u=u(x,y) по её обл. D,

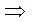
где Q’x=P’y (1) поступим следующим образом интегр. ПД du по ломаной которая параллельна осям координат и который соединяет произвольные фиксированные т. А с координатой А(x₀,y₀) с переменной т. М(x,y)

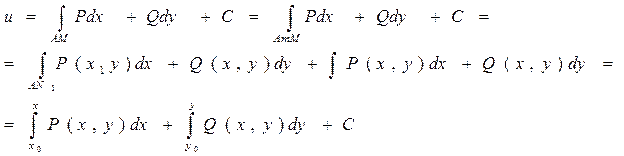(5)

2)

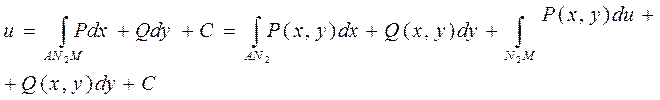(6)

Замечание: обычно в качестве начала точки А берёт начало координат А(0,0). Во многих случаях ф-ция u=u(x,y) по её ПД du=Pdx+Qdy можно найти иначе: (1)

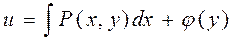(y-const)

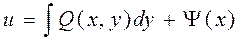2. (х-сonst), где 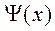и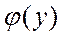

берём все известные числа из первого выражения и дополняем ими недостающие члены только от y из второго выражения, получаем ф-цию u проверяем если u=u(x,y) найдена верно то, u’x=P, u’y=Q.

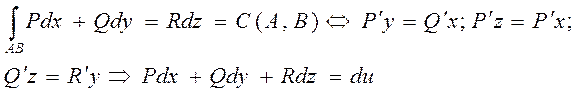Все условия сформулированные выше (теоремы 7.1 7.2 7.3) можно обобщить на случай когда КРИ вычисляется по пространственной прямой АВ:

Тогда

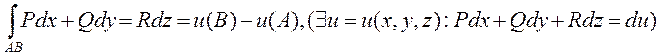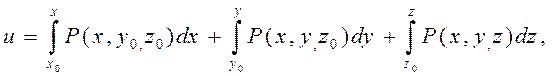Ф-ция u=u(x,y,z) определяется следующим образом (аналогично ф(5) и (6))

где т.(x₀,y₀,z₀) выбираем так чтобы записанные интегралы наиболее упрощались (чаще всего берут т. (0,0,0))

Л.8 Геометрическая и физические приложения КРИ 2-го рода

Дата добавления: 2014-01-11