Формула Стокса. Формула Стокса устанавливает связь между КРИ и ПВИ

Формула Стокса устанавливает связь между КРИ и ПВИ.

Теорема 11.2. Если функции P(x,y,z), Q(x,y,z), R(x,y,z) непрерывны вместе со своими ЧП-1 в точках ориентированной плоскости S, то имеет место формула:

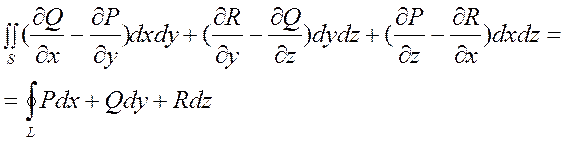(7)

L-гладкая замкнутая линия, граница которой поверхность S и интегрирование вдоль ^ прямой ведется в “+” направлении.

Замечание:

1) Формула Стокса выражает КРИ по замкнутому контуру через интеграл по поверхности натянутой на этот контур по этому применяется формула Стокса тогда, когда удобно заменить вычисление КРИ вычислением поверхностного интеграла.

2) Частным случаем формулы Стокса, когда L-гладкая замкнутая кривая на плоскости xOy, а поверхность S-часть плоскости xOy, ограниченной этим контуром L является формула Грина:

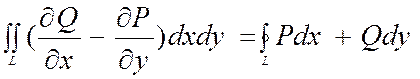
3) Из формулы Стокса следует, что при выполнении условий:

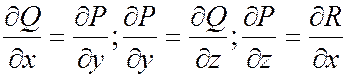
Из формулы Стокса следует, что КРИ по замкнутому контуру

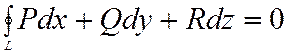при выполнений условия (3), а это означает, что КРИ не зависит от форму пути интегрирования.

11.3. Применение ПВИ к вычислению объёмов тел.

Вычислим V тела, ограниченного сверху гладкой поверхностью образующей параллельной оси Oz.

Запишем формулу Остраградского-Гаусса:

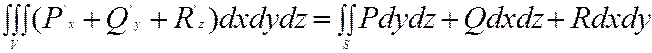
Пусть:

a) P=x,Q=0,R=0 Þ 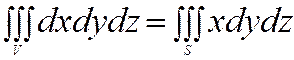(8)

б) P=0,Q=y,R=0 Þ (9)

в) P=0,Q=0,R=z Þ 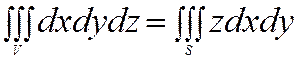(10)

(8)+(9)+(10) =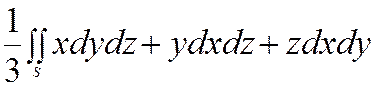

Дата добавления: 2014-01-11