Формула Остроградского-Гаусса

Лекция № 11.Связь между ПВИ, ТРИ и КРИ.

Формула Остроградского-Гаусса связывает ТРИ по некоторой пространственной области V с ПВИ по замкнутой поверхности S, ограничивающей данную область.

Теорема 11.1. Если функция Р(x,y,z), Q(x,y,z), R(x,y,z) непрерывны вместе со своими ИП-1 в пространственной области V, то имеет место формула:

(1)

S-замкнутая поверхность ограничевающая телоV и интеграл по поверхности S вычисляется по ее внешней стороне. (1)-формула Остроградского-Гаусса.

Пусть пространственная область V ограничивает снизу гладкой поверхностью S₁:z=f₁(x,y);сверху гладкой поверхностью S₂:z=f₂(x,y), причем функция f₁(x,y) и f₂(x,y) непрерывны в области D –проекции тела V на xoy; сбоку цилиндрическая поверхность S₃ с образующей параллельной oz инаправляющей-границей обл.D.

Вычислям ТРИ:

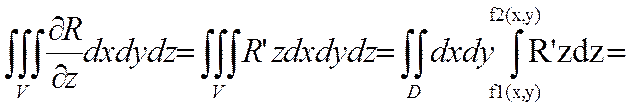
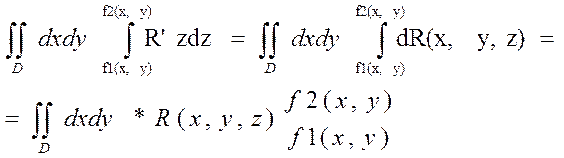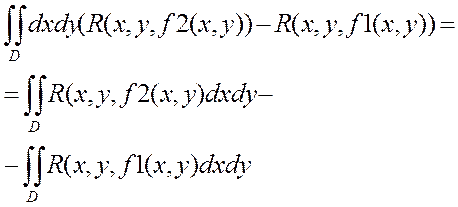= (2) ДВИ в правой части (2) можно рассмотреть как ПВИ-2 от ф.R(x,y,z)по внешней стороне поверхности S1и S2соответственно

Действительно,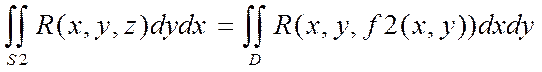

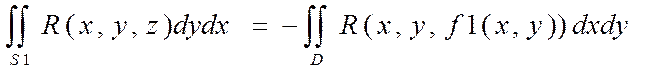
Тогда (2) запишется в виде: 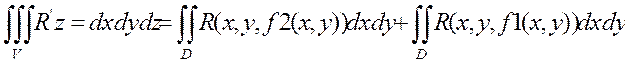(3)

Доставим к правой части (3) равный нулю ПВИ:

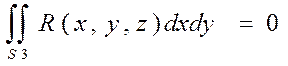
Тогда:

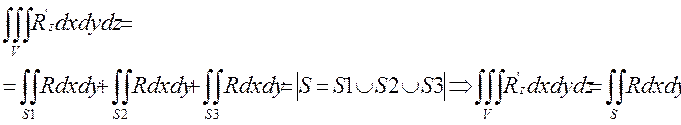(4)

Аналогично: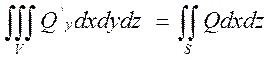 (5)

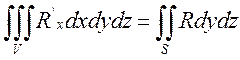(6)

Сложив правые и левые части (4),(5) и (6) получим: 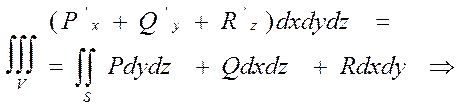формула

Остроградского-Гаусса

S-замкнутая поверхность, ограничивающая тело V.

Замечания:

1) Формула О-Г остаётся справедливой и для произвольной области V,т.к. её всегда можно разбить на подобласти рассматриваемого типа.

2) Формула О-Г является аналогом формулы Грина, которая связывает ДВИ по плоской области D с КРИ по контуру этой области.

3) Формулу О-Г удобно использовать для вычисления ПВИ-2 по замкнутым поверхностям.

Дата добавления: 2014-01-11