Л.20. Геометрический смысл модуля и аргумента производной. Понятие о конформном отображении

Теорема(обобщенная ф-ла Коши)

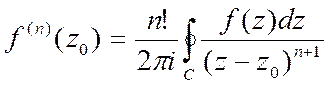Если ф-ция w=f(z) аналитической в односвязной обл. D, ограниченная замкнутым контуром С, а так же в точке самого этого контура, то n-ая производная этой ф-ции имеет вид:

(8)

Ф-лы (7) и (8) применяются при вычислении ИФКП, которые подинтегральную ф-цию можно представить в виде отношения аналитической ф-ции f(z) и выражения (z-z₀).

Пусть функция w=f(z) аналитична в точке z₀ и f’(z₀)≠0. Эта функция отображает точку z₀ в комплексной плоскости z в точку w₀=f(z₀) в комплексной плоскости w.

По определению производной в точке z₀ можно сказать, что

F’(z₀)=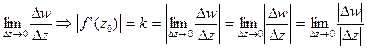

Этот предел не зависит от кривой l, т.к. функция f(z) – аналитическая и w->0 произвольным образом.

∆z=|z-z₀| - расстояние между точками z₀+∆z и z₀

∆w=|w-w₀| - расстояние между точками w₀+∆w и w₀

Величина k представляет собой предел отношения между расстоянием между отображенными точками w и w₀ к расстоянию между точками z и z_0.

Геометрический смысл модуля производной:

Величина k=|f’(z₀)| определяет коэффициент растяжения (подобия) в точке z₀ при отображении ∆w=f(z). Величина k называется коэффициентом растяжения, если модуль |f’(z₀)|>1 или коэффициентом сжатия, если |f’(z₀)|<1.

Это свойство называется свойством постоянства растяжений в точке.

Пример:

найти коэффициент растяжения (сжатия) для функции w=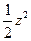, в точке z=3-4i.

Функция w аналитична во всех точках комплексной плоскости z.

w’=(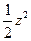)’=z

|w’|_z=3-4i|=|z|_z=3-4i|=|3-4i|=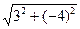=5>0

Значит, коэффициент растяжения функции равен 5.

Для аргумента производной в точке z₀ имеем:

argf’(z₀)=

=arg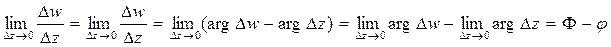,где

Φ – угол наклона к действительной оси касательной в точке w₀ к кривой L.

φ - угол наклона касательной к действительной оси в точке z₀ к кривой l.

Φ=φ+argf’(z₀)

Геометрический смысл аргумента производной:

Величина argf’(z₀) – угол, на который нужно повернуть касательную в точке z₀ к кривой l, чтобы получить направление касательной в точке w₀ к кривой L – образу кривой l при отображении w=f(z).

Если выбрать две кривые l₁ и l₂, проходящие через точку z₀ и найти их образы L₁ и L₂ при отображении w=f(z), то угол

следовательно, угол между кривыми L₁ и L₂ – образами кривых l₁ и l₂ равен углу между их праобразами l₁ и l₂. Это свойство сохранения величин углов и направления их отсчета называется свойством сохранения (консерватизма) углов в точке z₀.

Отображение w=f(z), обладающее свойством сохранения углов и постоянства растяжений в точке z₀ называется конформным отображением.

Вывод: Если функция w=f(z) – аналитична в точке z₀ и f’(z₀)≠0, то такое отображение w=f(z) конформно в точке z₀.

Опр.2: Отображение w=f(z) называется конформным в области D, если оно конформно в каждой точке этой области.

Дата добавления: 2014-01-11