Л.21. Ряды в комплексной области

21.2 Числовые ряды (ЧР):

Пусть z₁, z₂,…, z_n - последовательность комплексных чисел, где

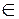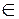(z_nC, nN)

Опр 1. Выражение видаz₁+z₂+…+z_n +…=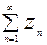(1)называется ЧР в комплексной области, причем z₁, z₂,…, z_n – члены числового ряда, z_n – общий член ряда.

Опр 2. Сумма n первых членов комплексного ЧР:

S_n=z₁+z₂+…+z_n называется n-ной частичной суммой этого ряда.

Опр 3. Если существует конечный предел при n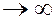последовательности частичных сумм S_n числового ряда, то ряд называется сходящимся, приэтом само число S называется суммой ЧР. В противном случае ЧР называется расходящимся.

Исследование сходимости ЧР с комплексными членами сводится к исследованию рядов с действительными членами.

Необходимый признак сходимости:

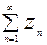сходится

Опр4. ЧР называется абсолютно сходящимся, если сходится ряд из модулей членов исходного ЧР: |z₁|+|z₂|+…+| z_n |+…=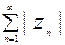

Этот ряд называется модульным, где |z_n|=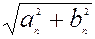

Теорема (об абсолютной сходимости ЧР): если модульный ряд 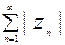, то сходится и ряд .

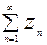При исследовании сходимости рядов с комплексными членами применяют все известные достаточные признаки сходимости знакоположительных рядов с действительными членами, а именно, признаки сравнения, Даламбера, радикальный и интегральный признаки Коши.

21.2 Степенные ряды (СР):

Опр5. СР в комплексной плоскости называется выражение вида:

c₀+c₁z+c₂z²+…+c_nzⁿ=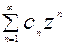, (4) где

c_n – коэффициенты СР (комплексные или действительные числа)

z=x+iy – комплексная переменная

x, y – действительные переменные

Также рассматривают СР вида:

c₀+c₁(z-z₀)+c₂(z-z₀)²+…+c_n(z-z₀)ⁿ+…=,

Который называется СР по степеням разности z-z₀, где z₀ фиксированное комплексное число.

Опр 6. Множество значений z, при которых СР сходится называется областью сходимости СР.

Опр 7. Сходящийся в некоторой области СР называется абсолютно (условно) сходящимся, если сходится (расходится) соответствующий модульный ряд.

Теорема (Абеля): Если СР сходится при z=z₀¹0 (в точке z₀), то он сходится, и притом абсолютно для всех z, удовлетворяющих условию: |z|<|z₀|. Если же СР расходится при z=z₀,то он расходится при всех z, удовлетворяющих условию |z|>|z₀|.

Из теоремы следует, что существует такое число R, называемое радиусом сходимости СР, такое, что для всех z, для которых |z|<R– ряд сходится и притом абсолютно, а для всех z, для которых |z|>R – СР расходится.

Областью сходимости СР является внутренность круга |z|<R с радиусом R и центром в начале координат на комплексной плоскости z. На границе этой области, т.е. на окружности |z|=R вопрос о сходимости СР решается дополнительным исследованием.

Если R=0, то СР сходится только в точке z=0.

Если R=¥, то областью сходимости СР является вся комплексная плоскость.

Областью сходимости СР является внутренность круга |z-z₀|<R с центром в точке z₀ и радиусом R.

Радиус сходимости СР определяется формулами:

R=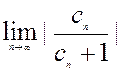 или R=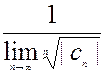

21.3 Ряд Тейлора:

Пусть функция w=f(z) аналитична в круге z-z₀<R, тогда в этом круге ее можно единственным образом представить в виде СР:

f(z)= =C₀+c₁(z-z₀)+c₂(z-z₀)²+…+c_n(z-z₀)ⁿ+…(*)

коэффициенты которой вычисляются по формуле:

c_n=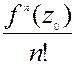, n=0,1,2,…

Такой СР (*) называется рядом Тейлора для функции w=f(z) по степеням z-z₀ или в окрестности точки z₀. С учетом обобщенной интегральной формулы Коши коэффициенты ряда (*) Тейлора можно записать в виде:

C_n=, где

C – окружность с центром в точке z₀, полностью лежащая внутри круга |z-z₀|<R.

При z₀=0 ряд (*) называется рядом Маклорена. По аналогии с разложениями в ряд Маклорена основных элементарных функций действительного переменного можно получить разложения некоторых элементарных ФКП:

1). e^z = 1+

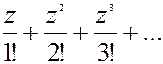
2). sin z = z-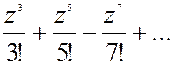

3). cos z = 1-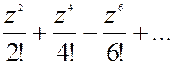

Разложения 1-3 справедливы на всей комплексной плоскости.

4). (1+z)^a = 1+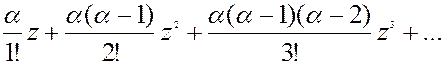

5). ln(1+z) = z-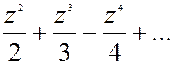

Разложения 4-5 справедливы в области |z|<1.

Подставим в разложение для e^z вместо z выражение iz:

e^iz=1+

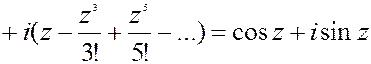(формула Эйлера)

21.4 Ряд Лорана:

Ряд с отрицательными степенями разности z-z₀:

c_-1(z-z₀)^-1+c_-2(z-z₀)^-2+…+c_-n(z-z₀)^-n+…=(**)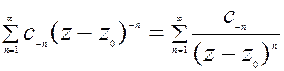

Подстановкой 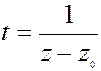ряд (**) превращается в ряд по степеням переменной t: c_-1t+c_-2t²+…+c_-ntⁿ+… (***)

Если ряд (***) сходится в круге |t|<r, то ряд (**) сходится в области |z-z₀|>r.

Образуем новый ряд как сумму рядов (*) и (**) изменяя n от -¥ до +¥.

…+c_-n(z-z₀)^-n+c_-(n-1)(z-z₀)^-(n-1)+…+c_-2(z-z₀)^-2+c_-1(z-z₀)^-1+c₀+c₁(z-z₀)¹+c₂(z-z₀)²+…

…+c_n(z-z₀)ⁿ= (!)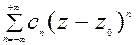

Если ряд (*) сходится в области |z-z₀|<R, а ряд (**) – в области |z-z₀|>r, то областью сходимости ряда (!) будет общая часть этих двух областей сходимости, т.е. кольцо (r<|z-z₀|<R), с центром в точке z₀, ограниченное окружностями |z-z₀|=r и |z-z₀|=R, которое называется кольцом сходимости ряда.

Пусть функция w=f(z) – аналитическая и однозначная в кольце (r<|z-z₀|<R),(0£r<R<¥), то в этом кольце ее можно единственным образом представить в виде ряда (!):

f(z)= ,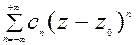

коэффициенты которой определяются по формуле:

C_n= (#), где

С – окружность с центром в точке z₀, которая полностью лежит внутри кольца сходимости.

Ряд (!) называется рядом Лорана для функции w=f(z).

Ряд Лорана для функции w=f(z) состоит из 2-х частей:

w=f(z)= =+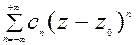

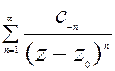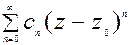
Первая часть f₁(z)= 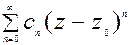(!!) называется правильной частью ряда Лорана. Ряд (!!) сходится к функции f₁(z) внутри круга |z-z₀|<R.

Вторая часть ряда Лорана f₂(z)= 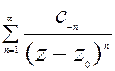(!!!) - главная часть ряда Лорана. Ряд (!!!) сходится к функции f₂(z) вне круга |z-z₀|>r.

Внутри кольца ряд Лорана 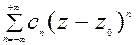сходится к функции f(z)=f₁(z)+f₂(z). В некоторых случаях или главная, или правильная часть ряда Лорана может или отсутствовать, или содержать конечное число членов.

На практике для разложения функции в ряд Лорана обычно не вычисляют коэффициенты С_n (#), т.к. она приводит к громоздким вычислениям.

На практике поступают следующим образом:

1). Если f(z) – дробно-рациональная функция, то ее представляют в виде суммы простых дробей, при этом дробь вида 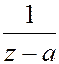, где a-const раскладывают в ряд геометрической прогрессии с помощью формулы:

1+q+q²+q³+…+=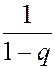, |q|<1

Дробь вида 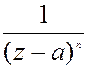раскладывают в ряд, который получается дифференцированием ряда геометрической прогрессии (n-1) раз.

2). Если f(z) – иррациональная или трансцендентная, то используют известные разложения в ряд Маклорена основных элементарных ФКП: e^z, sinz, cosz, ln(1+z), (1+z)^a.

3). Если f(z) – аналитическая в бесконечно удаленной точке z=¥, то подстановкой z=1/t задача сводится к разложению функции f(1/t) в ряд Тейлора в окрестности точки 0, при этом z-окрестностью точки z=¥ считается внешность круга с центром в точке z=0 и радиусом равным r (возможно r=0).

СОДЕРЖАНИЕ

Л.1 ДВОЙНОЙ ИНТЕГРАЛ В ДЕКАТОВЫХ КООРД.

1.1 Основные понятия и определения

1.2 Геометрический и физический смысл ДВИ.

1.3 основные свойства ДВИ

1.4 Вычисление ДВИ в декартовых координатах

Л.2 ДВИ в ПОЛЯРНЫХ КООРДИНАТАХ.ЗАМЕНА ПЕРЕМЕННЫХ в ДВИ.

2.1 Замена переменных в ДВИ.

2.2 ДВИ в полярных координатах.

Л.3Геометрические и физические приложения ДВИ.

3.1 Геометрические приложения ДВИ.

3.2 Физические приложения двойных интегралов.

1.Масса. Вычисление массы плоской фигуры.

2.Вычисление статических моментов и координат центра тяжести(центра масс) пластины.

3. Вычисление моментов инерции пластины.

Л.4ТРОЙНОЙ ИНТЕГРАЛ

4.1 ТРИ:основные понятия. Теорема существования.

4.2 Основные св-ва ТРИ

4.3 Вычисление ТРИ в декартовых координатах

Л.5 КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ПО КООРДИНАТАМ II РОДА – КРИ-II

5.1 Основные понятия и определения КРИ-II, теорема существования

5.2 Основные свойства КРИ-II

5.3 Вычисление КРИ – II для различных форм задания дуги АВ.

5.3.1 Параметрическое задание пути интегрирования

5.3.2. Явное задание кривой интегрирования

Л. 6. СВЯЗЬ МЕЖДУ ДВИ и КРИ. СВ-ВА КРИ II-го РОДА СВЯЗАННЫЕ с ФОРМОЙ ПУТИ ИНТЕГР.

6.2. Формула Грина.

6.2. Условия (критерии) равенства нулю контурного интеграла.

6.3. Условия независимости КРИ от формы пути интегрирования.

Л. 7Условия независимости КРИ 2-го рода от формы пути интегрирования (продолжение)

Л.8 Геометрическая и физические приложения КРИ 2-го рода

8.1 Вычесление S плоской фигуры

8.2 Вычисление работы переменой силы

Л.9 Поверхностные интегралы по площади поверхности (ПВИ-1)

9.1. Основные понятия, теорема существования.

9.2. Основные свойства ПВИ-1

9.3.Гладкие поверхности

9.4.Вычисление ПВИ-1 свидением к ДВИ.

Л.10. ПОВЕРХН. ИНТЕГРАЛЫ по КООРД.(ПВИ2)

10.1. Классификация гладких поверхностей.

10.2. ПВИ-2: определение, теорема существования.

10.3. Основные свойства ПВИ-2.

10.4. Вычисление ПВИ-2

Лекция № 11.СВЯЗЬ МЕЖДУ ПВИ, ТРИ и КРИ.

11.1.Формула Остроградского-Гаусса.

11.2 Формула Стокса.

11.3. Применение ПВИ к вычислению объёмов тел.

ЛК.12 ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ

12.1 Теор. Поля, осн. Понятия и определения.

12.2 Скалярное поле.

Л. 13 ВЕКТОРНОЕ ПОЛЕ (ВП) И ЕГО ХАР-КИ.

13.1 Векторные линии и векторные поверхности.

13.2 Поток вектора

13.3 Дивергенция поля. Формула Остр.-Гаусса.

13.4 Циркуляция поля

13.5 Ротор (вихрь) поля.

Л.14 СПЕЦ. ВЕКТОРНЫЕ ПОЛЯ И ИХ ХАР-КИ

14.1 Векторные дифференциальные операции 1 порядка

14.2 Векторные дифференциальные операции II – порядка

14.3 Соленоидальное векторное поле и его свойства

14.4 Потенциальное (безвихревое) ВП и его свойства

14.5 Гармоническое поле

Л.15 ЭЛЕМЕНТЫ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО. КОМПЛЕКСНЫЕ ЧИСЛА(К/Ч).

15.1. К/ч определение, геометрическое изображение.

15.2 Геометрическое представление к/ч.

15.3 Операция над к/ч.

15.4 Понятие расширенной комплексной z-пл.

Л.16 ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ КОМПЛЕКСНЫХ ЧИСЕЛ. Функция комплексного переменного (ФКП) и её приделы.

16.1. Последовательность комплексных чисел определение, критерий существования.

16.2 Арифметические свойства приделов комплексных чисел.

16.3 Функция комплексного переменного: определение, непрерывность.

Л.17 Основные элементарные ф-ции комплексного переменного (ФКП)

17.1. Однозначные элементарные ФКП.

17.1.1. Степенная ф.-ция: ω=Zⁿ.

17.1.2. Показательная ф.-ция: ω=e^z

17.1.3. Тригонометрические ф.-ции.

17.1.4. Гиперболические ф.-ции (shZ, chZ, thZ, cthZ)

17.2. Многозначные ФКП.

17.2.1. Логарифмическая ф.-ция

17.2.2. arcsin числа Z наз. число ω,

17.2.3. Обобщенная степенная показательная ф.-ция

Л.18Дифференцирование ФКП. Аналитич. ф-ия

18.1. Производная и дифференциал ФКП: основные понятия.

18.2. Критерий дифференцируемости ФКП.

18.3. Аналитическая функция

Л. 19 ИНТЕГРАЛЬНОЕ ИСЧЕСЛЕНИЕ ФКП.

19.1 Интеграл от ФКП(ИФКП):опр., сведение КРИ, теор. существ.

19.2 О существов. ИФКП

19.3 Теор. Коши

Л.20. Геометрический смысл модуля и аргумента производной. Понятие о конформном тображении.

20.1 Геометрический смысл модуля производной

20.2 Геометрический смысл аргумента производной

Л.21. Ряды в комплексной области.

21.2 Числовые ряды (ЧР)

21.2 Степенные ряды (СР):

21.3 Ряд Тейлора

21.4 Ряд Лорана

Дата добавления: 2014-01-11