
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Показательный закон распределения
|
|
|
|
Непрерывная случайная величина X имеет показательный (или
экспоненциальный) закон распределения, если ее плотность вероятно-
сти имеет вид
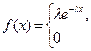
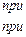
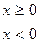 (2.35)
(2.35)
где  > 0 параметр распределения.
> 0 параметр распределения.
График плотности f(х) приведен на рис. 32.

Функция распределения показательного распределения имеет вид
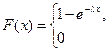
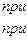
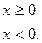 (2.36)
(2.36)
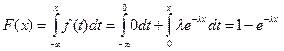
График F(x) представлен на рис. 33.

Найдем математическое ожидание и дисперсию показательного
распределения:
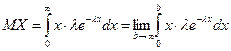 =[интегрируем по частям] =
=[интегрируем по частям] =
=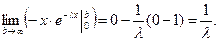
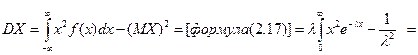
=[дважды интегрируем по частям]=
=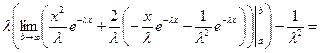
=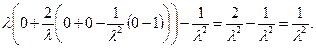
Таким образом,
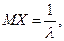
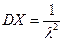 ,
, 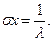 (2.37)
(2.37)
Найдем вероятность попадания случайной величины X, распределен-
ной по показательному закону, в интервал (а,b). Используя форму-
лу (2.2) и формулу (2.36), получаем
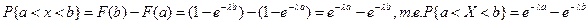
Пример 2.12. Случайная величина Т – время работы радиолампы
имеет показательное распределение. Найти вероятность того, что лам-
па проработает не менее 800 часов, если среднее время работы радио
лампы 400 часов.
О МТ = 400, значит (формула (2.37)),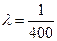 Искомая вероятность
Искомая вероятность
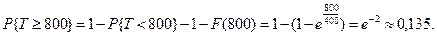
Показательное распределение используется в приложениях теории
вероятностей, особенно в теории массового обслуживания (ТМО), в фи-
зике, в теории надежности. Оно используется для описания распреде-
ления случайной величины вида: длительность работы прибора до пер-
вого отказа, длительность времени обслуживания в системе массового
обслуживания и т.д.
Рассмотрим, например, н. с. в. Т — длительность безотказной ра-
боты прибора. Функция распределения с. в. Т, т. е.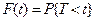 ,
,
определяет вероятность отказа за время длительностью t. И, значит,
вероятность безотказной работы за время t равна . Функция R(t) называется функцией надежности.
. Функция R(t) называется функцией надежности.
Случайная величина Т часто имеет показательное распределение.
Ее функция распределения имеет вид 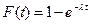 (формула (2.36)).
(формула (2.36)).
В этом случае функция надежности имеет вид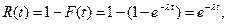 т.е.
т.е. 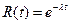 ,где
,где — интенсивность отказов, т. е. среднее число отказов в единицу времени.
— интенсивность отказов, т. е. среднее число отказов в единицу времени.
Показательный закон — единственный из законов распределения,
который обладает свойством «отсутствия последствия» (т. е. если про-
межуток времени Т уже длился некоторое время 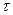 , то показатель-
, то показатель-
ный закон распределения остается таким же и для оставшейся части
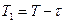 промежутка).
промежутка).
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1980; Нарушение авторских прав?; Мы поможем в написании вашей работы!