Равномерный закон распределения

Непрерывная с. в. X имеет равномерное распределение на отрезке
[а, b], если ее плотность вероятности f(x) постоянна на этом отрезке, а вне его равна нулю:

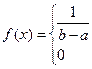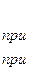
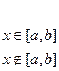, (2.32)

(т. е. f(x)=c при , но

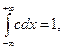
отсюда следует, что 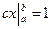, вместо отрезка [а, b] можно

писать (а, b) или (a, b], [а,b), так как с. в. X — непрерывна.)

График плотности f(x) для равномерного распределения н. с. в. X
изображен на рис. 28.

Равномерное распределение с. в. X на участке [a, b] (или (а, b)) бу-
дем обозначать:

Найдем функцию распределения F(x) для X~R[a,b ]. Согласно
формуле (см. п. 2.4)

f(x)
Ь — а	I I	■ ■
	а	ъ	X

Рис. 28

Имеем =

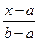
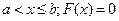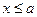при при ,и

при х > b. Таким образом,

(2.33)

График F(x) изображен на рис. 29

Рис. 29

Определим МХ и ОХ с. в. X ~ R[а, b].
Согласно формуле (2.11),

(Ожидаемый результат: математическое ожидание с. в. X ~ R[а, b]
равно абсциссе середины отрезка; МХ совпадает с медианой, т.е..)

Согласно формуле (2.14),

=

Таким образом, для н. с. в. X ~ R[а, b] имеем

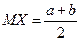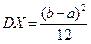, (2.34)

Пример 2.11. Пусть с. в. X ~ R(а,b). Найти вероятность попадания
с. в. X в интервал (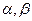), принадлежащий целиком интервалу (а, b).

О Согласно формуле (2.8), имеем

т.е.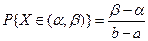

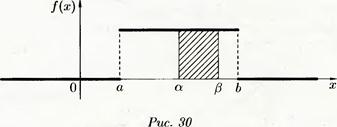
Геометрически эта вероятность представляет собой площадь пря-
моугольника, заштрихованного на рис. 30. •

К случайным величинам, имеющим равномерное распределение,
относятся: время ожидания пассажиром транспорта, курсирующего с
определенным интервалом; ошибка округления числа до целого (она
равномерно распределена на отрезке [—0,5; 0,5]). И вообще случайные величины, о которых известно, что все ее значения лежат внутри некоторого интервала и все они имеют одинаковую вероятность (плотность).

Дискретная случайная величина X имеет равномерное распреде-
ление., если она принимает целочисленные значения 1, 2, 3,..., п с
вероятностью где т = 1,2,3,..., п.

В этом случае 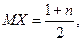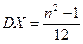Так, при п = 5,

многоугольник распределения имеет вид, представленный на рис. 31.
МХ = 3.

V 0,2
	1 2 3 4 5 *

Рис. 31

Дата добавления: 2014-01-11