Жорданова клетка. Циклический базис. Циклические пространства

Пусть степень корневого подпространства k равна размерности этого подпространства. В корневом пространстве 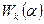найдется вектор e, минимальный аннулирующий многочлен которого равен 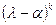(чтобы убедиться в этом, достаточно вспомнить, что минимальный многочлен подпространства равен наименьшему общему кратному минимальных многочленов базисных векторов). Система векторов 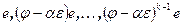линейно независима и, значит, является базисом 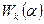. Базис данного вида называется циклическим. Пространство, в котором возможен циклический базис, называется циклическим пространством. Матрица линейного преобразования в циклическом базисе имеет вид 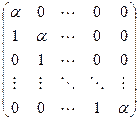. Действительно, образ базисного вектора 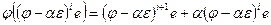, и, значит, при i < k- 1 раскладывается по двум базисным векторам, а при i = k -1 справедливо равенство 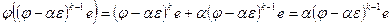. Матрица указанного вида называется нижней треугольной жордановой клеткой порядка k. Для получения верхней треугольной жордановой клетки циклический базис запишем в обратном порядке.

Теорема 1.5. Корневое подпространство раскладывается в прямую сумму циклических подпространств, размерность которых не превосходит степени минимального многочлена.

Доказательство проведем индукцией по размерности корневого подпространства. Если размерность корневого подпространства равна 1, то утверждение теоремы очевидно. В предположении, что утверждение теоремы верно для всех корневых пространств размерности не выше n -1, покажем его справедливость для n -мерного корневого пространства 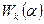, где k – степень минимального аннулирующего многочлена. Если k = n, то утверждение теоремы верно (все пространство циклическое). Пусть k < n. В корневом пространстве 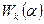найдется вектор e, минимальный аннулирующий многочлен которого равен 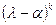. Дополним линейно независимую систему векторов до базиса корневого пространства векторами 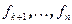. Линейную оболочку 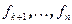обозначим через U. В пространстве U определим линейное преобразование 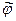: 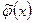- есть проекция вектора на подпространство U параллельно линейной оболочке 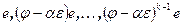. Многочлен 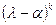является аннулирующим многочленом пространства U для 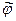. Действительно, для вектора x из U справедливо равенство 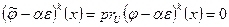. Таким образом, пространство U является корневым для преобразования 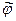и имеет размерность меньше n, следовательно, по предположению индукции пространство U разлагается в прямую сумму циклических подпространств. 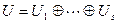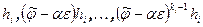Пусть и - циклический базис i -го слагаемого (i =1,…, s). Поскольку степень минимального многочлена преобразования 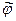не превосходит k, то 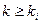(i =1,…, s). Из равенства 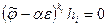вытекает, что вектор принадлежит линейной оболочке векторов 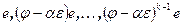и, следовательно, 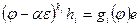, где 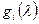- многочлен степени не выше k. Применив к обеим частям равенства преобразование 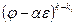, получим 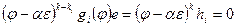, то есть многочлен 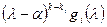является аннулирующим для вектора e. Аннулирующий многочлен вектора без остатка делится на минимальный аннулирующий многочлен вектора, следовательно, 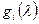делится без остатка на 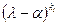, т.е. 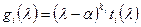. Тем самым установлено равенство 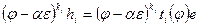, которое запишем в виде 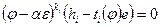. Положим 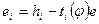, где (i =1,…, s). Для доказательства теоремы достаточно показать, что система векторов образует базис 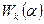. Поскольку общее количество векторов в системе равно n, то достаточно показать ее линейную независимость. Допустим, что 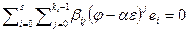(здесь полагаем 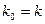и ). Спроектируем обе части равенства на U параллельно линейной оболочке векторов 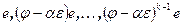и получим равенство 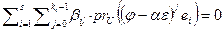. Поскольку , то получаем равенство , из которого вытекает 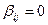при i >0, так как система векторов 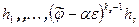образует базис U. Далее, из равенства 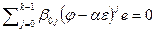, в силу линейной независимости системы 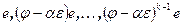, получаем равенство нулю остальных коэффициентов. Тем самым теорема доказана.

Дата добавления: 2014-01-11