Изоморфизм групп

Группа G с операцией * называется изоморфной группе H с операцией o, если существует взаимно однозначное соответствие 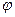, сохраняющее операции. То есть .

Например, группа G ={0,1} с операцией сложение по модулю 2 изоморфна группе H={1,-1} с операцией умножения *.

Группа называется конечной, если число ее элементов конечно. Число элементов группы называется порядком группы.

Теорема 2.1. Конечная группа порядка n изоморфна некоторой подгруппе симметрической группы n -го порядка.

Доказательство. Перенумеруем элементы группы. Через 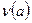обозначим номер элемента a. Отображение является взаимно однозначным, то есть перестановкой. Действительно, из равенства 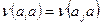вытекает . Умножив последнее равенство справа на 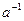получаем 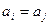, или i = j. Сопоставим элементу группы a перестановку . Указанное соответствие является взаимно однозначным. Действительно, из равенства перестановок 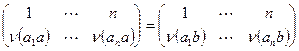вытекает равенство , которое выполняется только если 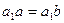. Умножив полученное равенство слева на получим a = b. Данное соответствие сохраняет операцию. Поскольку при произведении перестановок и имеем 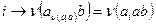, то 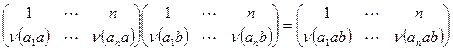, т.е. отображение сохраняет операцию. Для доказательства теоремы осталось заметить, что множество перестановок вида образуют подгруппу в симметрической группе. Действительно, замкнутость по умножению показана выше, а замкнутость при взятии обратного элемента вытекает из равенства .

Из приведенной теоремы вытекают простые факты:

1. С точностью до изоморфизма группа второго порядка единственна

2. С точностью до изоморфизма группа третьего порядка единственна

3. С точностью до изоморфизма существует только две группы четвертого порядка.

При больших n пользоваться данной теоремой затруднительно.

Дата добавления: 2014-01-11