Кольцо матриц. Эквивалентность матриц

Рассмотрим кольцо матриц порядка n с элементами из кольца K. Будем считать, что кольцо K с единицей. Элемент 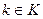называется обратимым, если найдется 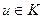, что 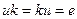(т.е. для него существует обратный элемент).

Матрица 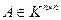называется унимодулярной, если для нее существует обратная с элементами из кольца K (т.е. матрица A является обратимым элементом кольца матриц).

Теорема 6.1. Матрица 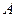является унимодулярной тогда и только тогда, когда ее определитель есть обратимый элемент кольца .

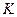Доказательство. Не сложное.

Свойство 6.1. Произведение унимодулярных матриц – унимодулярная матрица.

Доказательство. Следует из того, что произведение обратимых элементов – обратимый элемент .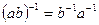

Свойство 6.2. Следующие преобразования со строками равносильны умножению слева на унимодулярную матрицу:

1. перестановка строк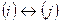

2. умножение строки на обратимый элемент кольца

3. прибавление к строке 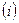строки 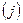, умноженной на элемент кольца .

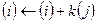Аналогичные преобразования со столбцами равносильны умножению справа на унимодулярную матрицу.

Доказательство. Выписать матрицу элементарного преобразования и показать ее унимодулярность.

Матрицы 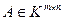и 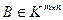называются эквивалентными, если найдутся унимодулярные матрицы 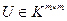и 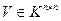, что A=UBV.

Пусть K – евклидово кольцо (т.е. в нем определена операция деления с остатком).

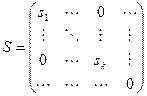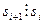Матрица , где при 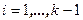называется нормальной диагональной формой Смита.

Теорема 6.2. Для любой матрицы 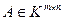существует эквивалентная ей нормальная диагональная форма Смита.

Доказательство. Достаточно привести матрицу с помощью элементарных преобразований (Свойство 6.2) к нормальной диагональной форме Смита.

Обозначим через 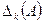- наибольший общий делитель миноров k -го порядка матрицы A.

Лемма 6.1. Пусть 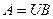, тогда .

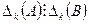Доказательство. Строки матрицы A являются линейными комбинациями строк матрицы B. Следовательно, по свойствам определителя (его линейности), любой минор k -го порядка матрицы A является линейной комбинацией миноров k -го порядка матрицы B, и, значит, .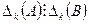

Следствие 6.1. Пусть 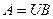, где 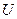- унимодулярная матрица. Тогда .

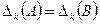Доказательство. Следует из равенств 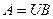, 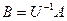и Лемма 6.1.

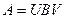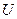Следствие 6.2. Пусть , где и 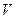- унимодулярные матрицы. Тогда .

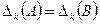Доказательство. По Следствие 6.1 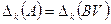. Далее 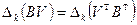и 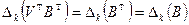(Следствие 6.1), следствие доказано.

Теорема 6.3. Нормальная диагональная форма единственна.

Доказательство. Пусть A эквивалентна нормально диагональной форме Смита S. Тогда 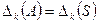, где 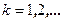. Следовательно, 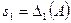, , 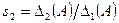…, 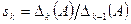. Все элементы нормальной диагональной формы Смита определены однозначно.

Дата добавления: 2014-01-11