ТЕМА 8. Меры повышения безопасности мореплавания

ТЕМА 7. Обработка избыточной информации при определении места судна

ТЕМА 6. Оценка точности места судна

ТЕМА 5. Обоснование метода выбора обсервации

ТЕМА 4. Использование методов математической статистики в судовождении

ТЕМА 3. Математический анализ и обработка навигационной информации

ТЕМА 2. Сферическая тригонометрия

ТЕМА 1. Вспомогательные сведения из математики

1.1. Некоторые правила и приемы приближенных вычислений. 5

1.2. Тригонометрические функции малых углов. 8

1.3. Интерполяция. 9

2.1. Основные определения и понятия. 13

2.2. Взаимополярные треугольники. 16

2.3. Теоремы сферической тригонометрии. 17

2.4. Решение сферических треугольников. 21

3.1. Случайные величины.. 24

3.2. Числовые характеристики случайных величин. 25

3.3. Основные законы распределения случайных величин. 26

3.4. Системы случайных величин. 30

3.5. Случайные функции, случайные процессы.. 33

4.1. Статистические оценки числовых характеристик случайных величин. 35

4.2. Погрешности навигационной информации. 38

4.3. Обработка измерений навигационных параметров. 42

4.4. Доверительная оценка случайной величины.. 45

4.5. Оценка точности функции измеренных аргументов. 47

5.1. Навигационная информация. 48

5.2. Навигационные параметры.. 51

5.3. Изолинии навигационных параметров. 53

5.4. Обобщенный метод линий положения. 55

5.5. Градиент навигационного параметра. 56

5.6. Определение места судна обобщенным методом линий положения. 59

6.1. Оценка точности обсервации по двум независимым линиям положения 61

6.2. Влияние систематической погрешности в линиях положения на обсервованное место. 62

6.3. Эллипс погрешностей. 64

6.4. Расчет элементов эллипса погрешностей. 66

6.5. Круговая погрешность места судна. 69

7.1. Использование избыточной информации при определении места судна 72

7.2. Совместный учет счисления и обсервации. 75

7.3. Последовательный метод наименьших квадратов. 77

7.4. Оптимальный фильтр Калмана. 79

8.1. Требования ИМО к точности судовождения. 81

8.2. Оценка навигационной безопасности в стесненных для плавания районах 85

Приложение 1. Вопросы к контрольной работе № 1. 90

Приложение 2. Вопросы к контрольной работе № 2. 91

Литература. 92

ТЕМА 1. вспомогательные сведения из математики

1. брол

абан

1.1. Некоторые правила и приемы приближенных вычислений

Во многих научных и инженерных задачах из-за сложности, а часто и невозможности точных решений применяются приближенные методы решения, к которым относятся: приближенное решение урав­нений, интерполяция, вычисление функций одного или нескольких переменных с помощью рядов, приближенное вычисление интегра­лов и др.

Ошибки арифметических действий с приближенными числами. Главным требованием к приближенным расчетам является соблю­дение заданной точности промежуточных вычислений и конечного результата. При этом в одинаковой степени недопустимы как уве­личение погрешностей (ошибок) путем неоправданного загрубления расчетов, так и удержание избыточных цифр, не соответствующих фактической точности. Ошибки, получающиеся при вычислениях и округлении чисел, разделяются на абсолютные и относительные. Абсолютной ошибкой приближенного числа называется абсолют­ная величина разности между приближенным а и точным А значе­ниями числа:

.

Как правило, абсолютная ошибка D_а неизвестна, поскольку неизвестно точное значение числа А. Поэтому в качестве ошибки принимают какую-либо оценку абсолютной ошибки

,

где D_{а пред} - предельная ошибка, задаваемая с учетом того, с какой достоверностью известно число а.

Относительной ошибкой числа а называется отношение его абсолютной ошибки D_а к абсолютной величине числа а:

.

Относительную ошибку также часто выражают в процентах:

Характеристика точности результатов с помощью относительной ошибки применяется во многих технических расчетах. Важным ее свойством является то, что величина этой ошибки остается неизменной при пропорциональном изменении самого приближенного числа и его абсолютной ошибки.

При операциях с приближенными числами ошибки результатов зависят от ошибок самих чисел. Далее рассмотрим закономерности изменения ошибок вычислений при различных арифметических действиях.

Ошибки суммы. Абсолютная ошибка суммы равна сумме абсолютных ошибок слагаемых:

.

Относительная ошибка суммы имеет величину

.

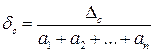Она заключена между минимальной и максимальной относительными ошибками слагаемых.

Ошибка разности. Абсолютная ошибка разности двух чисел равна суме абсолютных ошибок уменьшаемого и вычитаемого:

.

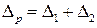Относительная ошибка разности определяется из выражения

.

Необходимо отметить, что когда значения а₁ и а₂ близки по величине, знаменатель выражения будет стремиться к нулю и ошибка d_р может оказаться неправдоподобно большой. В этом случае как d_р следует принять большую из относительных ошибок вычитаемого и уменьшаемого.

Ошибки произведения. Абсолютная ошибка произведения D_пр равна его относительной ошибке d_пр, умноженной на само произведение:

.

Относительная ошибка произведения определяется как сумма относительных ошибок сомножителей:

.

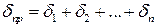Из формул и следует, что при умножении приближенного числа а на число N, свободное от ошибок, абсолютная ошибка D_пр возрастает в N раз, а относительная ошибка не изменяется. Действительно, если r = aN (D_N = 0 и d_N = 0), то d_пр = d_а.

А так как , получаем .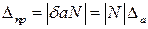

Ошибки частного. Абсолютная ошибка частного D_ч равна произведению относительной ошибки d_ч частного на его величину:

.

Относительная ошибка частного равна сумме относительных ошибок делимого и делителя:

.

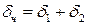Частное вида 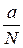, где N – безошибочное число, имеет абсолютную ошибку, в N раз меньшую, чем ошибка D_а: .

Ошибки степени. Если приближенное число а возводится в n -ю степень, то абсолютная ошибка степени D_ст равна относительной ошибке d_а числа, умноженной на произведение степени аⁿ на ее показатель n:

.

Относительная ошибка степени вычисляется по формуле

.

Ошибки корня. Абсолютная ошибка корня приближенного числа а равна произведению относительной ошибки d_а числа на корень этого числа, деленный на показатель n:

.

Приведенные выше формулы составлены так, что при вычисле­ниях по ним, как правило, происходит накопление ошибок, в то время как фактически в процессе расчетов ошибки приближенных чисел в значительной степени компенсируются.

Обычно ошибки промежуточных результатов не подсчитываются. Чтобы обеспечить достаточную точность конечного результата, рекомендуется придерживаться следующих правил подсчета необ­ходимого количества знаков.

· При сложении и вычитании приближенных чисел результат должен содержать столько десятичных знаков, сколько их имеет число с наименьшим количеством таких знаков.

· При умножении и делении приближенных чисел результат должен состоять из стольких значащих цифр, сколько их имеет число с наименьшим количеством таких цифр.

· При возведении приближенного числа в степень должно быть сохранено такое количество значащих цифр, какое их имеет возводимое в степень число.

· При извлечении корня резуль­тат должен быть выражен таким количеством значащих цифр, сколь­ко их в подкоренном числе.

Лишние знаки числа исключаются путем округления. Его про­изводят по правилам, называемым правилами дополнения:

· когда первая из отбрасываемых цифр меньше пяти, последнюю из оставляемых цифр не изменяют: 2,39724» 2,3972;

· когда первая отбрасываемая цифра больше пяти, последний со­храняемый знак числа увеличивают на единицу: 0,09186» 0,0919;

· когда первая отбрасываемая цифра равна пяти, а последующие знаки — нули, то последнюю оставляемую цифру не изменяют, если она выражает четное число, и увеличивают на единицу, если — не­четное (округление до четного числа): 513,0250» 513,02; 78,2350» 78,24;

· при наличии после отбрасываемой пятерки значащих цифр, отличных от нуля, последнюю из оставляемых цифр следует увели­чить на единицу: 8419,3853» 8419,39.

Соблюдение правил дополнения обеспечивает округление чисел с ошибкой, не превышающей 0,5 единицы разряда последнего остав­ляемого в числе знака. Ошибка эта имеет положительный знак при округлении с избытком и отрицательный — при округлении с не­достатком.

В ходе вычислений округление промежуточных результатов надо выполнять, сохраняя вместе с верными одну сомнительную цифру. Но конечный результат округляется так, чтобы все цифры числа были верными.

1.2. Тригонометрические функции малых углов

Один из возможных способов вычисления с заданной точностью той или иной тригономе­трической функции угла a заключается в разложении функции в ряд Маклорена с последующим учетом определенного числа членов разложения:

При малых значениях угла a допустимо ограничиться для рас­чета функции только первыми членами разложения и принять: sin a = a; tg a = a; cos a = 1.

С учетом размерностей эти формулы записываются так:

Наиболее часто применимыми в навигации мерами углов являются градусная, радианная и временная. Для них справедливы следующие соотношения:

.

Выясним, при каком значении угла a формулы обеспечи­вают определение функций с заданной точностью, например с точ­ностью 0,1’, 1’ или же 6', т. е. 0,1°. Из теории рядов известно, что когда при расчетах ограничиваются каким-либо определенным коли­чеством членов знакочередующегося сходящегося ряда, то связан­ная с этим ошибка результата не превышает первого из отбрасывае­мых членов разложения. Будем считать, что, удерживая в формуле только первый член ряда, мы получим ответ с ошибкой, равной второму члену. Так, полагая sin a = a, имеем 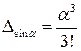, отсюда . Здесь величины D и a даны в радианах. Выразим ошиб­ку D в минутах дуги, а угол a — в градусах: 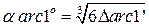. Подставляя числовые значения, получим: . При D = 1’ получим a = 6,9=6,9°.

Это означает, что заданная точность вычислений (D = 1’) по формуле sin a = a обеспечивается только при угле a, равном 6,9° или меньшем указанной величины. Результаты аналогичных вычислений для других тригонометрических функций смотрите в таблице 1.1.

Таблица 1.1 Предельные величины аргумента a при заданной точности вычислений тригонометрических функций

Расчетная формула	Предельная величина угла a при допустимой ошибке
0,1’	1’	6’ (0,1°)
sin a = a°arc 1°	3,2	6,9	12,5
tg a = a°arc 1°	2,5	5,5	9,9
cos a = 1	0,4	1,4	3,4

1.3. Интерполяция

Интерполяцией в вычислительной математике называют способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Интерполяцией пользуются при приближенном решении урав­нений, сглаживании рядов, приближенном интегрировании и в других задачах. В рутинных задачах судовождения интерполяция — вычис­ление значений табулированной функции для промежуточных (меж­ду табличными) значений аргумента.

Предположим, что в табличной форме задана непрерывная функ­ция у = f (х), причем значения функции y_i, y_i+1, …, y_n, соответст­вуют в таблице равноотстоящим значениям x_i, x_i+1, …, x_n аргумен­тов, называемых узлами интерполяции.

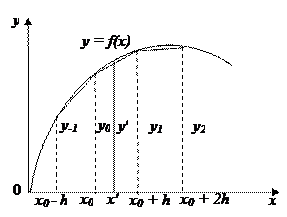
Рис. 1.1. Линейная интерполяция

Существует несколько видов интерполяции. Наиболее простая из них называется линейной. При линейной интерполяции делает­ся допущение, что коэффициент пропорциональности между прира­щением Dу функции и приращением Dх аргумента — величина по­стоянная. На рис. 1.1 функция у=f(х) показана штриховой лини­ей, а отрезки ломаной линии соответствуют линейной зависимости между аргументом и функцией в интервалах x_i+1-x_i, x_i+2-x_i+1 и т. д., которые называются шагом таблицы. Чем меньше шаг h, тем меньше различаются в данном интервале изображающая функ­цию кривая и заменяющая ее прямая линии. Именно с выбором ша­га связаны правомерность линейной (простой) интерполяции и ве­личины сопровождающих ее ошибок.

Пусть аргументу х₀ соответствует величина у₀ функции, ближай­шему к х₀ — меньшему или большему табличному аргументу х₁ — значение y₁ функции. Тогда шаг h таблицы выразится разностью h = x₁-x₀. Разность таблич­ных величин функции обозначим буквой D: D = y₁ - у₀.

Будем искать значение функ­ции у' для аргумента х', нахо­дящегося между табличными аргументами х₀ и х₁, т. е. х₀ < х' < х₁. С этой целью вы­числим величину Dх = х' — х₀, на которую аргумент х' отли­чается от табличного х₀, а затем составим пропорцию, принимая во внимание, что при изменении аргумента на h функция изменяется на величину D: Dx/h=Dy/D (здесь Dу — разность между приведенной в таблице величиной у₀ и искомым значением у' функции).

Найдя из пропорции величину Dу: 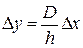, надо придать ее к табличному значению функции у₀: у' = у₀ + Dу.

В последней формуле величина Dу может быть как положи­тельной, так и отрицательной, что зависит от характера изменения функции при возрастании аргумента. Если по мере увеличения ар­гумента х функция у возрастает, величина Dу положительна; если же аргумент увеличивается, а функция уменьшается, то Dу отри­цательна. Поясним изложенное примером по данным табл. 1.2.

Таблица 1.2 Функция в табличном виде

X	y	D
x- 1 = 06°22’	y- 1 = 0,11089	0,00029
x0 = 06°23’	y0 = 0,11118
x 1 = 06°24’	y 1 = 0,11147	0,00029
x2 = 06°25’	y2 = 0,11176	0,00029

Пример. Требуется найти значение функции у' для аргумента х' = 06°23,4'.

Решение. 1. Вычислим приращение аргумента Dх относительно бли­жайшего табличного аргумента х₀:

.

2. Для составления пропорции определим шаг таблицы h и разность D табличных значений функции на аргументы х₀ и х₁:

.

3. Составив пропорцию, найдем Dу:

.

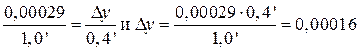4. Находим искомую функцию у':

у' = у₀ + Dу = 0,11118 + 0,00012 = 0,11130.

Наряду с линейной применяется также более точная интерполя­ция, называемая квадратичной, или параболической. Она предпо­лагает функциональную зависимость приращений аргумента и функции, геометрически описываемую параболой. Парабола, точ­нее ее участки между узлами интерполяции, лучше, чем прямоли­нейные отрезки, воспроизводит ту кривую, которая представляет заданную функцию у = f (x).

Квадратичная интерполяция выполняется путем расчетов по интерполяционным формулам. В качестве примера здесь приведе­ны две такие формулы, составленные по интерполяционным форму­лам Ньютона и Бесселя:

Формула применяется, если аргумент находится вблизи от начала таблицы, а формула используется, когда аргумент соответствует одному из средних интерполяционных узлов. В этих формулах для краткости введено обозначение U = Dx/h, остальные обозначения поясняются в табл. 1.3.

Таблица 1.3 Обозначения к формулам и

Аргумент	Функция	Разность
первая	вторая	третья
x-3 = x0 – 3h	y-3
x-2 = x0 – 2h	y-2
x-1 = x0 – h	y-1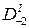
x0	y0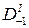
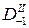
x1 = x0 + h	y1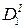
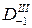
x2 = x0 + 2h	y2
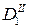
X3 = x0 + 3h	y3

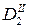
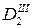
В обозначениях разностей римской цифрой указывается их по­рядок, а в нижнем индексе в условной форме даны номера строк, между которыми данная разность вычислена. Так, обозначение 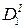отвечает первой разности значений у₀ и у₁ функции между строка­ми 0 и 1: .

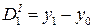Каждая вторая разность образуется из двух соседних по стро­кам значений первых разностей путем вычитания из большего числа меньшего. Например, . Подобным же образом опре­деляются разности других порядков. Через D_cp в формуле обозначено среднее арифметическое из разностей четного (второго) порядка по соседним строкам: .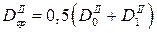

Математические таблицы мореходных посо­бий для плавания в основном составлены с такой точностью, что надобности в квадратичной интерполяции не возникает.

Воспользуемся интерполяционной формулой (по Бесселю) для того, чтобы выяснить, при каких условиях можно ограничивать­ся линейной интерполяцией, обеспечивая тем не менее требуемую точность приискания функции. Линейное интерполирование предпо­лагает учет только первых разностей. Это означает, что величины определяются по упрощенной формуле, в которой отброшены все члены более высокого порядка. Так, в формуле для линейной интерполяции надо сохранить только два слагаемых: .

Чтобы первое из отброшенных слагаемых 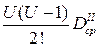(а значит, и все последующие) не влияло заметно на точность интерполяции, его величина не должна превышать 0,5 единицы последнего десятич­ного знака функции. Применительно к пятизначным математиче­ским таблицам это требование запишется так:

.

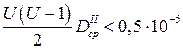Этим именно и определяется условие применения линейной интерполяции. Левая часть неравенства состоит из двух со­множителей. Сомножитель 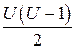зависит от шага h, выбираемо­го при составлении таблицы. Обозначим этот сомножитель В: 2В = U² — U. Экстремальное значение В_э, при котором выполня­ется условие, найдем, взяв производную и приравняв ее нулю:

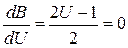, откуда U = ½.

Вторая производная 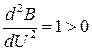показывает, что найден минимум и, следовательно,

.

Отсюда заключаем, что линейная интерполяция допустима, когда вторые разности не больше четырех единиц пятого десятичного знака: . Указанное условие, как правило, выполняется в мореходных таблицах.

Рассмотрим еще один вид интерполяции — линейную по методу наименьших квадратов. Предположим, что измерениями получено несколько значений функции y₁ = f(x₁); y₂ = f(x₂);…; y_n = f(x_n). Они представлены точками в прямоугольной системе координат. Поставим задачу – найти такую линейную функцию y = ax + b, для которой сумма квадратов отклонений значений функции y = f(x) от значений функции y = ax + b во всех точках с координатами (x_i, y_i) была бы наименьшей:

.

Чтобы при условии найти (и построить) интерполяционную линейную функцию, надо определить величины а и b. Для этого возьмем частные производные от F по а и b и сумму их приравня­ем нулю. После этого путем преобразований получим систему урав­нений

Отсюда и определяются коэффициенты а и b функции у = ах + b. Величина а — угловой коэффициент, выражающий тангенс угла наклона прямой по отношению к положительной оси координат; величина b называется начальной ординатой.

ТЕМА 2. Сферическая тригонометрия

2. а

2. а

2.1. Основные определения и понятия

Для решения многих задач судовождения используются формулы сферической тригонометрии. На основе таких формул составляют­ся, например, уравнения изолиний и градиентов некоторых нави­гационных параметров, алгоритмы для машинного решения задачи определения места судна; определяются величины углов и сторон параллактического треугольника с целью получения координат ме­ста судна и поправки компаса методами мореходной астрономии.

В навигации формулы сферической тригонометрии применяются, в частности, для расчета дуг больших кругов.

Ознакомимся с терминологией и важнейшими понятиями сфе­рической геометрии и тригонометрии.

Сферой называется замкнутая поверхность, все точки которой равно удалены от одной точки — центра О сферы.

Всякое сечение сферы плоскостью есть окружность. Принято эту окружность называть кругом.

Большим кругом называется след на поверхности сферы, кото­рый образуется при сечении ее плоскостью, проходящей через центр О. Через любую точку поверхности сферы может проходить бесчисленное множество больших кругов, радиус каждого из них равен радиусу сферы. Примерами больших кругов служат меридиа­ны и экватор координатной сетки на поверхности шара.

Полюсом большого круга называется точка поверхности сферы, лежащая на прямой, которая проходит через центр О сферы перпен­дикулярно плоскости большого круга. Каждый большой круг име­ет два полюса Р и Р' (рис. 2.1). Все точки большого круга равноудале­ны от его полюса на величину сферического радиуса.

Сферическим радиусом большого круга является дуга другого большого круга, проходящая от полюса Р (Р') до той или иной точки заданного большого круга. Сферический радиус большого круга равен 90°. На рис. 2.1 показаны сферические радиусы РК и РК'.

Рис. 2.1. Основные линии и точки на сфере

Дуги больших кругов (ДБК) обладают следующими свойствами: положение ДБК определяется двумя точками поверхности сферы (при условии, что эти точки не лежат на концах одного диаметра сферы); ДБК, заключенная между двумя точками сферы, является кратчайшим расстоянием между этими точками.

Из первого свойства следует, что через две точки поверхно­сти сферы можно провести дугу большого круга и причем только одну. Вообще дуга большого круга играет на поверхности сферы такую же роль, как и прямая на плоскости.

Малым кругом называется след на поверхности сферы, образуе­мый в результате сечения ее плоскостью, не проходящей через центр О сферы. К малым кругам, в частности, относятся параллели ко­ординатной сетки шара и круги равных высот светил. Каждый ма­лый круг имеет свои полюсы (Р"). Но сферический радиус малого круга не равен 90°.

Сферическим треугольником называется фигура на сфере, обра­зованная тремя пересекающимися попарно дугами больших кругов. Во всех задачах задаются и определяются элементы такого сфериче­ского треугольника, каждая сторона которого ограничена предела­ми 180° (Эйлеров треугольник).

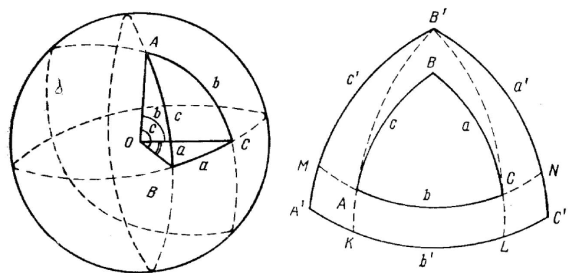
Рис. 2.2. Сферический треугольник

Рис. 2.3. Взаимно полярные сферические треугольники

На рис. 2.2 показан сферический треугольник с общепринятыми обозначениями его Эл ементов. Углы обозначены прописными бук­вами латинского алфавита А, В, С, а противолежащие углам сто­роны — соответствующими строчными. Точка О обозначает центр сферы и одновременно вершину трехгранника с плоскими углами а, b, с.

Так как длина дуги большого круга выражается произведением центрального угла и радиуса R сферы, то: .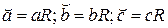

Принимая R = 1, заключаем, что стороны сферического тре­угольника измеряются плоскими углами а, b, с трехгранника. Сумма плоских углов трехгранника и, следовательно, сумма сторон сферического треугольника лежат в пределах

.

Когда сумма сторон становится равной нулю, треугольник пре­вращается в точку, а при a + b + c = 360° — в большой круг. Для сторон сферического треугольника справедливы неравенства вида: а + b > с; а — b < с и т. д.

Углы А, В, С сферического треугольника измеряются двугран­ными углами трехгранника. Так, угол А измеряется двугранным углом при точке О между плоскостями АОС и АОВ трехгранника. Иначе можно сказать, что угол А измеряется углом между каса­тельными AM и AN к сторонам b и с в вершине А треугольника. По свойствам двугранных углов трехгранника сумма углов А, В, С сферического треугольника имеет величину

,

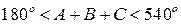или

.

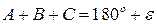Здесь выражено основное свойство сферического треугольника, заключающееся в том, что сумма его углов всегда больше 180° на величину сферического избытка (эксцесса) e. Величина самого сферического избытка больше 0°, но меньше 360°: 0° < e < 360°. В радианах сферический избыток имеет величину

.

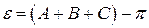Приведем без доказательств еще некоторые соотношения эле­ментов сферического треугольника:

· сумма двух углов без третьего угла меньше 180°, например: А + В — С < 180°, или А + С — В < 180°;

· против больших сторон треугольника лежат большие углы;

· против равных сторон лежат равные углы;

· площадь сферического треугольника выражается формулой

,

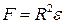где R — радиус сферы, ед. длины; e — сферический избыток, рад.

Сферические треугольники подразделяются на косоугольные, прямоугольные и четвертные (прямосторонние). У прямоугольного треугольника один из углов равен 90°. Когда у треугольника два прямых угла, он называется двупрямоугольным; возможен и трехпрямоугольный сферический треугольник. У четвертного треуголь­ника равна 90° одна из сторон.

Элементы сферических треугольников в практических зада­чах выражаются в градусной мере, а при рассмотрении теоретиче­ских вопросов — в радианной.

2.2. Взаимополярные треугольники

Пусть задан сферический треугольник ABC (рис. 2.3). Из вер­шины А как из полюса построим сферическим радиусом AM = 90° дугу а' большого круга. Точно так же из полюсов В и С сфериче­скими радиусами ВК и CL построим дуги b ' и с ' больших кругов. Эти три дуги, пересекаясь образуют новый сферический треуголь­ник с вершинами А ', В ' и С '. (Поскольку на рис. 2.3 у исходного треугольника ABC каждая из сторон предполагается меньше 90°, то он расположен внутри треугольника А'В'С'. В других случаях стороны треугольников будут пересекаться.) Далее из того же рисунка следует, что дуги C'N, В'М и A'L есть сферические ра­диусы сторон заданного тре­угольника ABC с полюсами в вершинах А ', В ' и С '.

Таким образом, имеем два сферических треугольника, у ко­торых вершины одного являют­ся полюсами сторон другого. Такие треугольники называют­ся взаимополярными.

Рассмотрим зависимость ме­жду элементами взаимополярных треугольников. С этой целью найдем сумму угла А внутреннего треугольника и стороны а ' внешнего. Из рис. 2.3: , следовательно .

Но сумма дуг 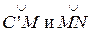— это сферический радиус стороны с внутреннего треугольника с полюсом в вершине С, а сумма дуг - сферический радиус стороны и с полюсом в вершине В'. Каждый радиус равен 90°. Поэтому

А + а' = 180°; В + b' = 180°; С + с' = 180°.

Полученные равенства выражают первое свойство элементов взаимополярных треугольников.

Для вывода второго свойства найдем сумму угла А ' внешнего и стороны а внутреннего треугольников. Угол А' измеряется ду­гой большого круга KL: А ' = 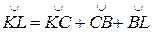. Поэтому А ' + а = 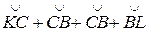, но 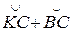= 90° и = 90° как сферические радиусы сторон b ' и с ' соответствен­но. Следовательно,

.

Свойства взаимополярных треугольников используются при вы­воде некоторых формул и при решении практических задач сфериче­ской тригонометрии.

2.3. Теоремы сферической тригонометрии

Задачей сферической тригонометрии является установление за­висимостей между сторонами и углами сферического треугольни­ка. Сферический треугольник считается заданным, если известны какие-либо три его элемента. Под решением треугольника подразу­мевается отыскание его неизвестных элементов. В большинстве случаев решение выполняется по так называемым основным форму­лам, к которым относятся: формула косинуса стороны; формула ко­синуса угла; формула синусов; формула котангенсов, называемая также формулой четырех рядом лежащих элементов.

Зависимости между элементами сферического треугольника, выражаемые первыми тремя формулами, называют теоремами.

Каждая формула связывает три известных (заданных) элемента с одним из неизвестных. Наряду с выводами основных формул ни­же приводится вывод однотипной с ними формулы пяти элементов.

Формула косинуса стороны (теорема косинусов). Построим сфе­рический треугольник ABC и трехгранник с вершиной в точке О (рис. 2.4). В вершине А проведем касательные к сторонам b и с тре­угольника. Касательные пересекутся в точках N и М с продолжен­ными ребрами трехгранника. Заметим, что все три ребра трехгран­ника равны радиусу R сферы.

Дважды используя теорему квадрата стороны плоского косо­угольного треугольника, найдем сторону NМ сначала из треуголь­ника NAM, а затем из треугольника NOM:

Рис. 2.4. Графические построения к выводу формул сферического треугольника

Теперь в плоских прямоугольных треугольниках NAO и МАО найдем гипотенузы NO и МО:

.

Подставим величину квадратов гипотенуз в выражения и приравняем правые части этих выражений: (NA)² + (MA)² – 2NA×MA cos A = (NA)² + (MA)² + R² – 2NO×MO cos a. Пос­ле приведения подобных членов и сокращения на 2 перегруппируем слагаемые и поделим их почленно на NO и МО: . Так как в плоских прямоугольных треугольниках NAO и MAO: 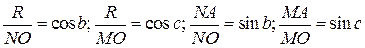, то окончательно получим .

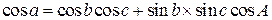Выведенная формула справедлива одновременно и для углов трехгранника, и для элементов сферического треугольника, мерой которых служат углы трехгранника.

Формула косинуса стороны читается так: в сферическом тре­угольнике косинус стороны равен произведению косинусов двух дру­гих сторон плюс произведение синусов этих сторон на косинус угла между ними (... на косинус угла, противолежащего исходной сто­роне).

Формула косинуса стороны связывает стороны и один из углов сферического треугольника. Всего таких формул три:

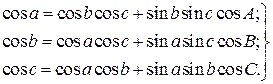
Формула косинуса угла (теорема косинусов для полярного тре­угольника). Эта формула выражает зависимость между тремя угла­ми и стороной сферического треугольника. Ее можно вывести, ис­пользуя свойства взаимополярного треугольника. Напишем форму­лу косинуса стороны а' одного из взаимополярных треугольников: cos a' = cos b' cos с' - sin b' sin с' cos A'.

Перейдем к элементам второго треугольника по первому и вто­рому свойствам: а' = 180° — A; b' = 180° — В; с ' = 180° — С; A ' = 180° — а. Подставив правые части этих равенств в исходную формулу, получим cos (180° — А) = =cos (180° — В) cos (180° — С) + sin (180° — В) sin (180° — С) cos (180° — а), или

Последние две формулы приведены без вывода. Читается формула косинуса угла следующим образом: косинус угла сферического треугольника равен отрицательному произведе­нию косинусов двух других углов плюс произведение синусов этих уг­лов на косинус стороны между ними (... на косинус стороны, противо­лежащей исходному углу).

Формула синусов (теорема синусов). Эта формула объединяет две стороны и два противолежащих им угла сферического треуголь­ника.

В трехграннике (рис. 2.4) из вершины С опустим перпендикуляр CL на грань АОВ. Из точки L проведем еще две вспомогательные прямые LK и LK': первую — под углом 90° к ребру ОВ, а вторую — под таким же углом к ребру ОА. Соединив точку С с точками К и К', получим два прямоугольных треугольника CKL и CК'L с общим ка­тетом CL, который равен CL = СК sin В в треугольнике CKL; CL = CK ' sin A в треугольнике СK'L, т. е.

.

Так как в двух других плоских прямоугольных треугольниках СКО и СК'О стороны СK и СК' являются катетами, то: СК = R sin а; СК ' = R sin b. После подстановки в формулу по­лучим R sin a sin В = R sin b sin А, или

.

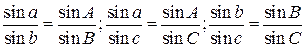Здесь последние две формулы составлены по аналогии с первой. Формулы выражают теорему синусов: в сферическом треуголь­нике синусы сторон относятся как синусы противолежащих углов.

Формула пяти элементов. Эта формула объединяет три стороны и два угла сферического треугольника. Выведем ее, пользуясь фор­мулами косинуса сторон а и b:

Подставим в первое выражение значение cos b:

cos a = (cos a cos с + sin a sin с cos B) cos с + sin b sin с ´ cos А.

Раскрыв скобки и перенеся слагаемые, содержащие cos a, в левую часть, получим cos a (l —cos² с) = sin a sin с cos с ´ cos B + sin b sin с cos A. Поделим все слагаемые на sin c: cos a sin с = sin a cos с cos B + sin b cos A. Поменяв слагаемые местами, получим формулу пяти элементов: sin b cos A — cos a ´ sin с — sin a cos с cos B.

Ее читают так: в сферическом треугольнике синус стороны, ум­ноженный на косинус прилежащего угла, равен произведению коси­нуса стороны, противолежащей этому углу, на синус третьей сто­роны минус произведение синуса противолежащей стороны на косинус третьей стороны и на косинус угла между ними.

Так как к каждой стороне треугольника примыкают по два уг­ла — один «слева», другой «справа», то всего можно написать шесть формул пяти элементов:

Выведем теперь формулу пяти элементов в другом варианте, когда она связывает три угла и две стороны треугольника. С этой целью напишем две формулы косинуса угла:

Сделаем преобразования, подобные предыдущим:

cos А = -(-cos A cos² C+ sin A cos С sin С cos b) + sin В sin С cos a;

cos A sin² C = -sin A cos С sin С cos b + sin В sin С cos a

и окончательно

sin В cos a = cos A sin C +sin A cos С cos b.

Таким образом, в сферическом треугольнике произведение сину­са угла на косинус прилежащей стороны равно произведению косинуса угла, противолежащего этой стороне, на синус третьего угла плюс произведение синуса противолежащего угла на косинус третьего-угла и на косинус стороны, противолежащей исходному углу.

Таких формул тоже шесть:

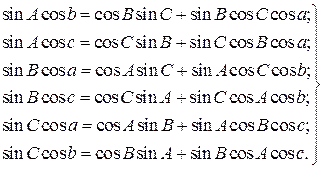
Формула котангенсов (формула четырех рядом лежащих элемен­тов). Эта формула связывает четыре элемента треугольника, распо­ложенных подряд. Для вывода возьмем какую-либо формулу пяти элементов, например

sin b cos A = cos a sin с — sin a cos с cos В.

По теореме синусов выразим величину синуса стороны b:

sin b = sin В sin a /sin A, и подставим ее в начальное выражение:

.

Поделив обе части на sin а, получим ctg A sin B = ctg a sin c - cos с cos В. Это и есть формула четырех рядом лежащих элементов. Выпи­шем объединяемые формулой элементы в том порядке, в каком они даны в треугольнике (рис. 2.4), начиная с угла A и заканчивая сто­роной а: А — с — В — а. В этой формуле элементы (буквы) A и a являются по расположению крайними, а элементы с и В — средни­ми. В связи с этим формулу четырех элементов принято читать так: произведение котангенса крайнего угла на синус среднего угла равно произведению котангенса крайней стороны на синус средней стороны минус произведение косинусов средних элементов.

Если от того же крайнего угла A перечислить подряд три эле­мента в противоположном направлении, то по тому же правилу мож­но составить вторую формулу четырех ря­дом лежащих элементов. А так как в ка­честве крайнего может быть любой из трех углов треугольника, то общее число фор­мул котангенсов равно шести:

2.4. Решение сферических треугольников

Решить треугольник означает по трем заданным элементам найти остальные три. Порядок решения с помощью калькулятора следующий.

Начертить треугольник и обозначить заданные элементы.

1. Подобрать теоремы и привести формулы к рабочему виду. Это означает перенести все известные в одну сторону уравнения и оставить функции только sin, cos, tg, т.е. только те функции, которые есть на клавиатуре калькулятора.

2. Произвести набор на клавиатуре калькулятора в соответствии с рабочей формулой.

3. Проанализировать ответ и записать его. Если ответ получился отрицательным, добавить к нему 180^о. Если вычисления производились по теореме синусов, определить четверть, в которой лежит найденный элемент, по величине противолежащего элемента (против угла больше 90^о лежит сторона больше 90^о и наоборот).

При подборе теорем рекомендуется пользоваться только тремя заданными элементами (так называемое, независимое решение) и не брать вновь найденные элементы.

Если при решении необходимо записывать промежуточные результаты, надо сохранять пять знаков после запятой.

Решение сферических треугольников в задачах судовождения

Покажем, как применяются теоремы сферической тригонометрии для решения конкретных судоводительских задач.

Судно совершает плавание по дуге большого круга из точки А в точку В. На рис. 2.5 показаны меридианы этих точек и экватор.

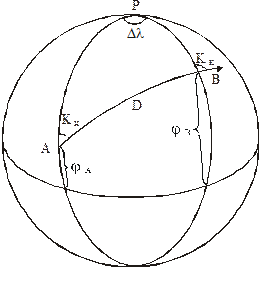
Рис. 2.5. Плавание по дуге большого круга

Точкой Р обозначен полюс. Координаты точек А и В заданы. Это означает, что известны стороны РА и РВ (дополнение соответствующих широт до 90^о) и сферический угол при полюсе (разность долгот). Требуется найти плавание D, курс начальный К _н и конечный – К _к.

Как видно на рис. 2.5, в сферическом треугольнике РАВ даны две стороны и угол между ними. Воспользуемся теоремами косинуса стороны и четырех рядом лежащих элементов.

cos D = cos (90^o - j _A) cos (90^o - j _B) + sin (90^o -_A) sin (90^o - j _B) cos;

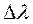ctg A sin 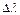= ctg (90^o - j _B) sin (90^o - j _A) - cos (90^o - j _A) cos ;

;

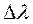ctg B sin = ctg (90^o - j _A) sin (90^o - j _B) - cos (90^o - j _B) cos ;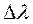

.

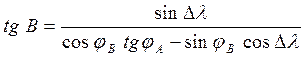Подставляя заданные координаты в рабочие формулы, и, находим D, А и В. На рис. 4 видно, что угол А равен начальному курсу, а конечный курс равен 180^о- В. Найденное значение D в градусах умножаем на 60, чтобы получить минуты, т.е. морские мили.

Следует иметь в виду, что в формулах − значение определяет величину сферического угла при полюсе безотносительно к полушарию восточному или западному, т.е. подставляется туда по модулю.

Рис. 2.6. Параллактический треугольник

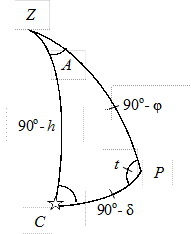
На рис. 2.6 схематично изображаем треугольник на небесной сфере, который называется параллактическим. Его решение заключается в нахождении высоты и азимута светила. Исходными данными являются: j, d и t.

Высоту светила находим по теореме косинуса стороны:

Для нахождения азимута воспользуемся теоремой котангенсов:

Следует заметить, что, так как в сферическом треугольнике ни один элемент не может быть больше 180^о, азимут получается в полукруговом счете и его перевод в истинный пеленг требует дополнительного анализа.

ТЕМА 3. Математический анализ и обработка навигационной информации

3. Рис 3

3. Б

3.1. Случайные величины

Случайная величина ─ это величина, которая может принимать то или иное значение неизвестное до опыта. Под случайной величиной понимают всю совокупность значений, которые она может принимать.

Если случайная величина Х измерена п раз, то значения (результаты измерений) называются ее реализациями в данной серии.

Случайная величина называется дискретной, если все ее значения можно перечислить. Например, количество очков на гранях игрального кубика, погрешности в 0,1^о при округлении поправки компаса.

Если случайная величина своими значениями заполняет некоторый числовой интервал, то она называется непрерывной. Например, площадь пробоины, время до первого отказа прибора.

Поскольку случайная величина может принимать различные значения, важно знать, с какой вероятностью могут появляться те или иные ее значения. Зависимость между самой случайной величиной и вероятностью появления ее возможных значений называется законом распределения случайной величины.

Закон распределения может быть представлен в трех видах: ряд распределения, функция распределения и плотность распределения.

Самый простой вид − ряд распределения. Он представляет собой таблицу, где каждому значению случайной величины соответствует вероятность ее появления:

х 1	х 2	х 3	…	хп
Р1	Р2	Р3	…	Р п

Естественно, что перечислить все x_i можно только для дискретных случайных величин и ряд распределения возможен только для них.

Второй вид − функция распределения F (x). Она показывает, чему равна вероятность того, что случайная величина не превосходит данное значение х, т.е. F (x) = Р(Х ≤ х).

Для того, чтобы найти F (x) надо суммировать вероятности всех значений Х ≤ х. Для дискретных величин это можно сделать простым суммированием, а для непрерывных − интегрированием от - ∞ до х. Поэтому F (x) называют еще интегральной функцией распределения.

Рис. 3.1. Функции распределения случайных величин: а) дискретная; б) непрерывная

Увеличивая Х, можно накрыть интервал всех возможных значений случайной величины, т.е. F (x) стремится к 1.

Третий вид, в котором может быть представлен закон распределения случайной величины, − плотность распределения f (x).

Рассмотрим рис. 3.1 б. Очевидно, что чем круче идет кривая F (x), тем бóльшие вероятности суммируются, т.е. для участков с более вероятными значениями кривая имеет больший наклон к оси Х. Тангенс угла наклона кривой есть производная от этой функции. Производная от функции распределения называется плотностью распределения: F' (x) = f (x).

Производную имеют только непрерывные функции, поэтому плотность распределения существует только для непрерывных случайных величин. На рис. 3.2 показана плотность распределения одной из случайных величин.

На графике плотности распределения хорошо видно, где наиболее вероятные значения случайной величины (около максимума f (x)), а где менее вероятные.

Вероятность того, что случайная величина заключена в пределах от a до β, равна площади под кривой в этом интервале и может быть найдена путем интегрирования:

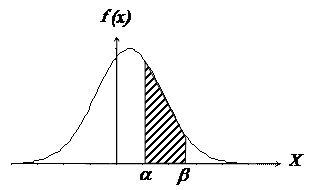
Рис. 3.2. Плотность распределения случайной величины.

Так как в интервале от - ∞ до + ∞ случайная величина какое-то значение принимает с неизбежностью, площадь под всей кривой f (x) равна 1. Плотность вероятности полностью характеризует случайную величину.

3.2. Числовые характеристики случайных величин

Закон распределения дает исчерпывающую характеристику случайной величины. Она задается графически или аналитически. Но ни график, ни формула не являются удобными для действий с величинами. Поэтому для их описания используют числовые характеристики. Обычно вполне достаточными являются две из них: математическое ожидание и дисперсия.

Математическое ожидание представляет собой центр, вокруг которого группируются все вероятные значения случайной величины. Для дискретных величин оно может быть подсчитано как сумма произведений всех значений случайной величины на соответствующие вероятности:

.

Для непрерывных величин суммирование заменяется интегрированием, а математическое ожидание определяется формулой

.

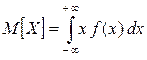Второй числовой характеристикой случайной величины является дисперсия D[ Х ]. По аналогии с физическим явлением (дисперсией света) дисперсия случайной величины представляет собой ее рассеяние вокруг математического ожидания. Чем больше дисперсия, тем больше рассеяния по числовой оси значений случайной величины.

Введем понятие центрированной случайной величины. Это разность между конкретным значением и математическим ожиданием случайной величины: х – М [ Х ]. Дисперсию можно представить, как математическое ожидание квадрата центрированной величины:

.

Для дискретных величин дисперсия может быть подсчитана по формуле

.

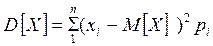Для непрерывных величин дисперсия определяется по формуле

.

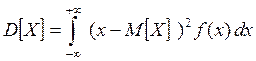Дисперсия имеет размерность квадрата случайной величины. Удобнее характеризовать разброс в тех же единицах, что и сама случайная величина. Поэтому от дисперсии переходят к среднему квадратическому отклонению

.

И математическое ожидание, и дисперсия, и среднее квадратическое отклонение, как и сама вероятность, могут определяться из опыта и имеют свои статистические аналоги.

3.3. Основные законы распределения случайных величин

Функции f (x), описывающие плотность распределения, могут быть различными. Рассмотрим те из них, которые часто встречаются в судовождении.

Равномерное распределение

При равномерном распределении все значения случайной величины равновероятны. Примером такого распределения может служить погрешность при округлении какого-либо числа. Графически равномерное распределение показано на рис. 3.3. Аналитически равномерное распределение представлено формулой

f (x) = const.

Так как площадь под кривой должна быть равной 1, то случайная величина распределяется на ограниченном интервале от a до β. Вне этого интервала f (x) = 0.

На рис. 3.3 видно, что площадь под кривой равна произведению f (x) на (β - a). Следовательно, f (x)· (β - a) = 1. Откуда

.

Рис. 3.3. Закон равномерного распределения.

Найдем числовые характеристики равномерно распределенной случайной величины. Математическое ожидание запишем на основании и:

.

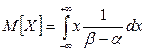После преобразований получим

.

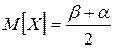Для определения дисперсии подставим выражения математического ожидания и плотности распределения в формулу:

.

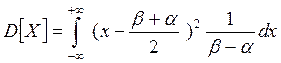После преобразований получим

Как уже говорилось, закон равномерной плотности справедлив при округлении чисел. Интервал, на котором распределены погрешности округления в 0,1 единицы последнего знака, заключен от a = − 0,5 до β = +0,5 этого знака. Подставив эти значения и в и, получим значения для математического ожидания и дисперсии:

или 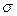= 0,29 единицы последнего знака.

Нормальный закон

Если на случайную величину действует множество причин, ни одна из которых не преобладает, то ее распределение подчиняется нормальному закону. Это наиболее часто встречающийся закон. Он описывает огромное количество самых различных случайных величин, в том числе все измерения. Поэтому в дальнейшем будем пользоваться им при обработке наблюдений.

Нормальный закон представлен графически на рис. 3.4 и аналитически формулой

.

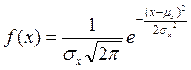где 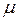_х − математическое ожидание случайной величины;

σ _х − ее среднее квадратическое отклонение.

Рис. 3.4. Нормальный закон распределения.

Анализируя формулу, видим, что плотность распределения максимальна, при показателе степени е равном 0, т.е. когда х =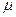 _х,. Математическое ожидание является наиболее вероятным значением и определяет центр кривой.

Если в подставить х = m_х,, получим максимальное значение плотности вероятности, равное 1/σ _х . Эта величина определяет высоту кривой. Чем больше σ _х , тем ниже максимум кривой, но так как площадь под кривой всегда равна 1, она становится более пологой, увеличивается вероятность больших отклонений. Таким образом, _х характеризует разброс случайной величины вокруг математического ожидания.

Чтобы вычислить вероятность того, что случайная величина попадет в интервал от a до β, надо в формулу подставить значение плотности вероятности из:

.

Численные методы интегрирования выражения для некоторых характерных интервалов дают следующие вероятности: 0,683 для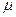± σ; 0,954 для 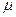± 2σ; 0,997 для 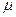± 3σ.

Значения вероятностей (например, 0,683) можно понимать двояко: либо, что ук

Дата добавления: 2014-01-11