Принципиальная возможность определить систематическую погрешность позволяет исключить ее из результатов измерений

Определение систематических погрешностей возможно различными способами. Теоретические и практические исследования позволили вывести зависимость астрономической рефракции от высоты светила, а наклонения горизонта от высоты глаза наблюдателя. Как правило, теоретические соображения позволяют определять методические погрешности.

Другим способом определения систематических погрешностей является их непосредственное измерение. Например, пеленгование створов позволяет определять погрешность компаса, погрешность индекса секстана определяется по горизонту, звезде или Солнцу, погрешность хронометра определяется по радиосигналам времени или сличением с гринвичским временем на экране GPS-приемника.

Систематическая погрешность может быть также определена методикой обработки измерений навигационных параметров. Для этого необходимы избыточные измерения.

После того, как систематическая погрешность тем или иным способом определена, она исключается из результата измерения. Делается это тремя способами. Наиболее распространенным способом является введение поправки в вычисления. Поправка равна погрешности с обратным знаком. Алгебраическая сумма результата измерения и поправки дает свободное от систематической погрешности значение навигационного элемента.

Примерами могут служить поправка компаса, поправка лага, поправка хронометра, поправка за астрономическую рефракцию, наклонение горизонта и т.д.

Вторым способом служит введение поправки в прибор. Например, введение поправки за скоростную погрешность в гирокомпасе, уменьшение поправки индекса секстана, перевод стрелок часов или хронометра.

Наконец, третий способ заключается в организации измерений. Примером может служить определение поправки лага на мерной линии с неизвестным вектором течения

Рис. 4.1. Распределения случайных погрешностей

Случайные погрешности − это погрешности, изменяющие свою величину и знак от наблюдения к наблюдению без каких-либо известных закономерностей. Они принципиально непредсказуемы, однако, как и любая случайная величина, они подчиняются определенному закону распределения, и эти законы могут быть использованы для уменьшения их влияния на результат измерения.

Случайные погрешности распределены, в основном, по нормальному закону и иногда по равномерному закону. Графики этих распределений показаны на рис. 3.3 и 3.4. Если начало отсчета на этих графиках перенести в математическое ожидание, получим распределения случайных погрешностей. Они показаны на рис. 4.1. На этом рисунке случайная погрешность обозначена 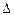. В обоих случаях графики симметричны относительно начала отсчета (нулевой погрешности), что говорит о том, что равные по величине, но противоположные по знаку погрешности равновероятны. Это важное свойство лежит в основе обработки измерений: в достаточно большой совокупности измерений случайные погрешности в значительной степени компенсируют друг друга.

Промахи. Частным случаем случайной погрешности является промах. На графике нормального закона видно, что большие по величине погрешности маловероятны. Вероятность того, что навигационный параметр будет измерен с отклонением от математического ожидания (погрешностью) больше тройного среднеквадратического отклонения, равна 0,003. Из тысячи измерений только три превысят этот предел. Этот предел (тройное среднеквадратическое отклонение) принят за условную границу допустимых отклонений. Все измерения, выполненные с бóльшими отклонениями, называются промахами (выбросами). Они исключаются из обработки и не влияют на конечный результат.

Полная погрешность. Систематическая погрешность исключается поправкой, которая определяется измерением или вычислением. И то, и другое содержит случайные погрешности, которые составной частью войдут в поправку. При дальнейшей обработке измерений, хотя поправкой и будет исключена систематическая погрешность, в результате останется ее случайная составляющая. Следовательно, при каждом использовании поправки результат будет искажаться на одну и ту же величину неучтенной случайной составляющей. Другими словами после исключения систематической погрешности в навигационных элементах все равно остается ее часть, хотя и меньшая.

Таким образом, в результате измерения после исключения систематической погрешности с помощью поправки всегда остается погрешность случайная и остаток систематической погрешности. Этот остаток совместно со случайной погрешностью образует полную погрешность.

В зависимости от соотношения величин случайной и систематической части полная погрешность проявляет себя по-разному. В случае явного преобладания случайной части измерения независимы. В случае явного преобладания систематической части измерения становятся функционально зависимыми. Наконец, если ни та, ни другая часть не преобладает явно, измерения являются вероятностно зависимыми и эта зависимость описывается корреляционным моментом или коэффициентом корреляции.

4.3. Обработка измерений навигационных параметров

Навигационным параметром называется геометрическая величина, связывающая координаты ориентиров с координатами точек на земной поверхности.

Измерения взаимозависимые и неравноточные

Для получения значения навигационного параметра достаточно одного измерения. Чтобы уменьшить влияния случайных погрешностей, делается серия измерений.

Допустим, измерена серия какого-либо навигационного параметра Х и после исправления поправками получены результаты х ₁, х ₂…. х_п. Измерения не равноточные. Точность каждого измерения оценим полной средней квадратической погрешностью (СКП) т_i. Обозначив искомое значение навигационного параметра через х _о, для каждого измерения можно записать уравнение

х _о» х_i.

В каждом результате измерения содержится полная погрешность V_i, состоящая из случайной и повторяющейся части. Чтобы получить точное значение навигационного параметра, эту погрешность из результата измерения надо вычесть:

х _о = х_i− V _i.

Таким образом, для п измерений будем иметь систему п уравнений вида

V_i = х_i− х _о,

которые называются уравнениями невязок.

Наиболее вероятное значение х _о будем искать в соответствии с принципом максимального правдоподобия. Для этого надо, чтобы совокупность невязок обладала наибольшей плотностью вероятности.

Обратимся к формуле представляющей плотность вероятности для системы произвольного количества случайных величин. В ней выражение, стоящее перед основанием натурального логарифма е, для данной совокупности − константа. Невязки входят в показатель степени:

.

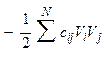Чтобы плотность вероятности была максимальной, надо отрицательный показатель степени е минимизировать, т.е. значение х _о надо выбрать таким, чтобы

.

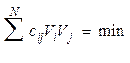Левая часть − однородный многочлен второй степени относительно невязок, называемый квадратичной формой. Поэтому метод определения неизвестного значения случайной величины наложением условия называется методом наименьшей квадратичной формы или обобщенным методом наименьших квадратов.

Для нахождения минимума необходимо производную функции приравнять к нулю. Подставив в выражения для невязок из, можно записать

.

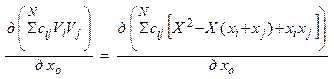Произведя дифференцирование, получим

.

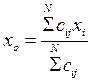В этой формуле N = п² − общее число слагаемых, c_ij − элементы матрицы, обратной к корреляционной.

,

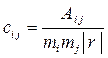где т − СКП навигационного параметра,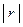− определитель, а А_ij − алгебраическое дополнение элементов определителя нормированной корреляционной матрицы

.

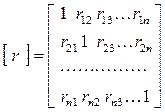Значение А_ij рассчитывается как определитель матрицы 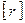с вычеркнутой i строкой и j столбцом.

Перейдем к оценке точности найденного значения навигационного параметра.

Точность навигационного параметра оценивается средней квадратической погрешностью, которая для зависимых неравноточных измерений вычисляется по формуле

,

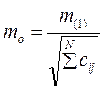где знаменатель вычисляется так же, как и в формуле, а числитель − СКП единицы элемента c_i., Она находится по формуле

.

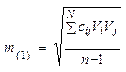При числе измерений меньше 5 формула дает большую погрешность. В этом случае принимают т ₍₁₎ = 1 и точность найденного навигационного параметра оценивают по формуле

.

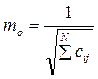Измерения независимые и неравноточные

Если измерения независимы, то коэффициенты корреляции в матрице, кроме диагональных, равны нулю. Тогда все не диагональные элементы А_ij и c_ij также равны нулю. Диагональные элементы А_ij равны 1, а диагональные элементы c_ij равны 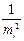. С учетом этого формула преобразуется к виду

.

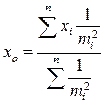Величина

.

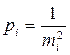называется весом и характеризует степень доверия к измерению. Чем меньше СКП измерения, тем больше его точность и вес.

С учетом формула примет вид

.

Погрешность среднего взвешенного оценивается по формуле

,

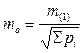где т ₍₁₎ − СКП измерения с весом 1, которая рассчитывается по формуле

.

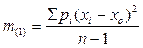Формулой (6.23) пользоваться при п < 5 не рекомендуется, так как она дает слишком неточный результат. При п < 5 принимают т ₍₁₎= 1 и СКП средневзвешенного рассчитывают по формуле

.

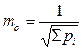Измерения взаимозависимые и равноточные

В этом случае наиболее вероятное значения рассчитывается по формуле

.

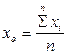Значение, полученное по формуле называется средним арифметическим.

Погрешность среднего арифметического, найденного по зависимым равноточным измерениям оценивается формулой

,

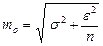где d - систематическая погрешность, e - случайная погрешность.

Измерения равноточные и независимые

Наиболее вероятное значение навигационного параметра определяется как среднее арифметическое по формуле. Эта формула используется в подавляющем большинстве случаев, потому что измерения, как правило, выполняются одним и тем же наблюдателем, одним и тем же прибором и в одних и тех же условиях. То есть измерения являются равноточными, причем справедлива эта формула и для зависимых, и для независимых измерений.

Погрешность среднего арифметического, рассчитанного по независимым измерениям определяется по формуле

,

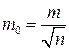где т − СКП измерения параметра.

4.4. Доверительная оценка случайной величины

Рассмотренные нами среднее арифметическое и средневзвешенное являются оценками наиболее вероятных значений случайных величин. А чему равна вероятность этих оценок? Оказывается, она равна нулю. Это, так называемый, парадокс нулевой вероятности. Заключается он в том, что для непрерывных случайных величин вероятность любого конкретного значения равна нулю.

Действительно, вероятность подсчитывается по формуле интегрированием на определенном отрезке числовой оси и равна площади под кривой закона распределения на этом отрезке. Площадь же появляется только, если на числовой оси взять отрезок. Если на числовой оси указать точку, площадь над ней равна нулю.

Поэтому наиболее вероятные значения называют точечными оценками случайной величины. Если же необходимо знать значение случайной величины с определенной вероятностью, например, 0,5, надо указать на числовой оси интервал, в котором содержится 50% всех возможных значений этой величины.

Обычно этот интервал указывается симметрично относительно среднего значения случайной величины. Величина вероятности на определенном интервале зависит от вида закона плотности распределения вероятности. Напомним, что для нормального закона вероятность нахождения случайной величины на отрезке х _о ± т равна 0,683; на отрезке х _о ± 2 т 0,954; на отрезке х _о ± 3 т 0,997.

С помощью таблицы «Функция Лапласа», которая есть «Мореходных таблицах», можно определить соответствие вероятности любому интервалу. Прямая и обратная выборки позволяют находить как вероятность по заданному интервалу, так и интервал для заданной вероятности. Этот интервал называется доверительной оценкой, а соответствующая ему вероятность − доверительной вероятностью. Величина вероятности показывает, насколько можно доверять этой оценке. Границы доверительного интервала называются доверительными границами.

Значение доверительного интервала задается в виде доверительных границ. Например, I _90%= (35,6^о; 37,2^о). Можно задать доверительный интервал, указав центр и полуширину интервала. Например, I _90%= 36,4^о±0,8^о. Иногда вместо термина «доверительная оценка» используется термин «интервальная оценка».

Значения в таблице «Функция Лапласа» рассчитаны для нормального закона распределения, причем подразумевается наличие бесконечного количества значений случайной величины. В серии измерений содержится определенное, как правило, небольшое количество измерений и доверительный интервал, рассчитанный по «оценочным параметрам» нормального закона, будет отличаться от теоретического, тем больше, чем меньше число измерений.

Зависимость величины интервала от числа измерений для нормального закона была изучена Стьюдентом и приведена в форме таблицы «Распределение Стьюдента». В ней аргументами служат число степеней свободы (число измерений минус единица) и доверительная вероятность. В таблице приводятся значения t − коэффициента кратности СКП. Умножив на этот коэффициент СКП, и отложив полученное значение влево и вправо от среднего, получим границы доверительного интервала. При числе измерений больше 20 распределение Стьюдента мало отличается от нормального.

4.5. Оценка точности функции измеренных аргументов

Если результат измерения, отягощенный погрешностью, используется для вычисления какой-либо функции, то и функция получается с погрешностью. Точность функции оценивается средней квадратической погрешностью. В общем случае функция зависит от нескольких аргументов и погрешности каждого искажают вычисленное значение функции.

Выясним зависимость СКП функции от СКП аргументов. Допустим, задана функция

z = f (x, y …).

Было произведено п измерений аргументов, по которым рассчитывается значения функции z. Обозначим погрешности в аргументах через 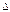x, 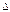у и т.д., а погрешность функции − 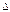z. Тогда каждому измерению будет соответствовать уравнение

z +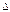 z_i = f (x + 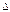x_i, y + 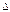у_i …).

Разложим правую часть в ряд Тейлора, ограничившись линейными членами, и вычтем из полученного равенства

.

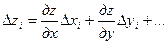Чтобы перейти от индивидуальных погрешностей к средним квадратическим, возведем равенство в квадрат, просуммируем все п уравнений и разделим на п – 1:

.

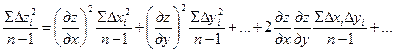Суммы квадратов погрешностей, деленные на п – 1, представляют собой квадраты СКП переменных, а суммы в слагаемых с коэффициентом 2 − корреляционные моменты соответствующих аргументов:

.

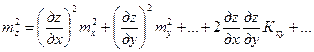Извлекая квадратный корень из обеих частей равенства, получим общую формулу СКП функции измеренных аргументов

.

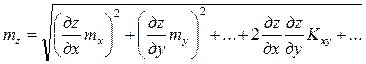Формула используется для взаимозависимых аргументов. Если аргументы независимы, корреляционные моменты становятся равными нулю и СКП функции рассчитывается по формуле

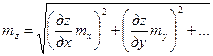
Таким образом, чтобы оценить СКП функции, надо определить ее частные производные по всем аргументам, содержащим погрешности и умножить их на СКП этих погрешностей.

Большинство формул, используемых в судовождении, являются одночленными выражениями, При их дифференцировании для нахождения частных производных полезно использовать следующий прием.

Если функция задана в виде

z = Ах^ту^п, то ; .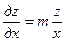

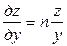Этот прием применим при любом количестве сомножителей, любых, в том числе отрицательных и дробных показателях степеней. Он позволяет значительно облегчить вычисления производных. При этом, что важно, при подстановке производных в формулу размерности переменных сокращаются с размерностями соответствующих СКП. Таким образом, размерность СКП функции получается одинаковой с размерностью самой функции.

Порядок вычислений СКП функции следующий.

1. Вычислить значение самой функции.

2. Вычислить частные производные функции по всем переменным.

3. Подставить найденные значения вместе с СКП в формулу.

4. Привести в соответствие друг другу размерности слагаемых под радикалом. На это следует обратить особое внимание, так как именно из-за этого происходят, в основном, ошибки в вычислениях.

5. Выполнить вычисления.

ТЕМА 5. Обоснование метода выбора обсервации

5. А

5. Б

5.1. Навигационная информация

Элементы навигационной информации

Навигационной информацией являются сведения, которые определяют положение судна и его элементы движения. Величины, составляющие навигационную информацию, называются навигационными элементами. Все навигационные эле­менты получаются в результате измерений или вычислений на основе измерений. Это обстоятельство определяет случайный характер навигационных элементов и требует вероятностного подхода к их оценке.

К навигационной информации относятся следующие навигацион­ные элементы.

Координаты судна. Координаты судна могут быть выбраны относительно экватора и гринвичского меридиана (географические координаты), относительно какого-либо подвижного или неподвижного объекта (полярные), относительно линии пути (маршрутные).

Навигационные параметры — это измеряемые величины, завися­щие от взаимного расположения судна и ориентира и служащие для определения места судна.

Элементы счисления включают в себя все величины, позволяющие вычислить местоположение судна на любой момент времени: истинный курс судна, угол дрейфа, вектор скорости течения, скорость хода, интервал времени, для которого производится расчет координат.

Поправки технических средств судовождения и методические поправки. Это наиболее многочисленный вид навигационной информации. Он включает в себя поправку компаса, поправку лага, поправку хронометра, магнитное склонение и девиацию магнитного компаса, ортодромическую поправку, наклонение видимого горизонта, поправки к координатам карт с разными геодезическими системами и т. д.

Измеренные моменты времени ─ это показания хронометров, часов и секундомеров в заданный момент.

Классификация информации

Навигационная информация классифицируется по нескольким признакам.

Однородная информация и неоднородная информация. Однородная информация получается в результате измере­ний, основанных на одном и том же физическом принципе. Например, несколько компасных пеленгов, измеренных пеленгатором компаса, высоты нескольких светил, измеренные секстаном; ряд астрономических поправок компаса, и т. п.

Разнородная информация получается в результате измере­ний, основанных на различных физических принципах. Например, расстояние до ориентира, измеренное с помощью радиолока­тора, и расстояние, вычисленное по вертикальному углу; курс по гирокомпасу и курс по магнитному компасу. Разнородными являются также навигационные элементы, имеющие разное наименование: пеленг и высота, расстояние и глу­бина и т. п.

Равноточная и неравноточная информация. Равноточными являются измерения, выполненные одним и тем же наблюдателем одним и тем же прибором и в одних и тех же условиях.

Информация считается неравноточной, если навигацион­ные элементы измерены с различной точностью.

По виду измерений информация делится на непосредственно измеренную и косвенно измеренную. Непосредственно измеренная информация является прямым результатом процесса измерения: например, высота светила, измеренная секстаном; пеленг, измеренный с помощью пеленгатора компаса; курсо­вой угол, измеренный путем визирования ориентира; глубина, изме­ренная ручным лотом, и т. п.

Косвенно измеренная информация является функцией непосредственно измеренных физических параметров и вычисляется или преобразуется на основании результатов измерений. Например, расстояние в радиолокаторе вырабатывается преобра­зованием измеренного времени распространения радиоимпульса от судна до ориентира; по измеренному вертикальному углу и высоте ориентира рассчитывается расстояние до него; глубина, измеренная эхолотом, получается преобразованием времени распространения ультразвукового сигнала до дна и обратно и т.п.

По степени полноты информация подразделяется на неполную, необходимую и избыточную.

Неполная информация не позволяет определить искомые навигационные элементы. Например, один навигационный параметр не позволяет определить место судна.

Необходимая информация обеспечивает расчет искомых навигационных элементов. В необходимой информации столько измерений, сколько неизвестных элементов.

Избыточная информация ─ это информация, полученная сверх необходимой. Например, третий навигационный параметр при определении места судна, второе и последующие измерения одного и того же навигационного эле­мента. Избыточная информация не является бесполезной, она позволяет ослабить влияние случайных погрешностей.

Исходная и итоговая информация. Исходной информацией являются результаты измерений или выбранные из таблиц значения, подлежащие дальнейшей обработке в целях получения навигационных элемен­тов.

Итоговая информация − это значения навигационных элементов, которые получаются в результате обработки некоторой исходной информации. Одна и та же информация в одном случае может быть исходной, в другом − итоговой. Так например, при определения места судна координаты являются итоговой информацией, а при вычислении элементов сноса по обсервациям − исходной.

По степени взаимозависимости информация делится на независимую, стохастически зависи­мую и функционально зависимую.

Понятия независимой, стохастически зависимой или функционально зависимой информации может относиться только к группе навигационных элементов. Информация является независимой, если каждый навига­ционный элемент рассматриваемой совокупности формируется под воздействием только своих частных случайных факторов.

Если наряду с частными факторами в формировании навига­ционных элементов участвует хотя бы один общий случайный фак­тор, то информация является стохастически зависимой. Если же все рассматриваемые навигационные элементы форми­руются только общими случайными факторами, то такая информация функционально зависимая.

По характеру измерения информация делится на дискретную и непрерывную. Дискретная информация ─ это информация, измеренная через определенные интер­валы времени. Например, отсчеты, снимаемые со шкалы нави­гационного прибора.

Непрерывная информация измеряется без перерывов в течение некоторого интервала времени. Как правило, непрерывная информация записывается на лентах самописцев, например, на курсографной ленте гирокомпаса.

5.2. Навигационные параметры

Для обеспечения безопасности во время перехода судоводитель должен постоянно контролировать место судна. По путевому углу и пройденному расстоянию на любой момент времени можно вычислить местоположение судна. Такой способ определения места судна называется счислением, а само место − счислимым.

Из-за погрешностей в направлении движения и пройденном расстоянии с течением времени счислимое место становится все более неопределенным и возникает необходимость его уточнения. Сделать это можно относительно ориентиров, положение которых хорошо известно. Определение места судна по ориентирам называется обсервацией, а место, полученное таким образом, − обсервованным. Ориентиры могут быть естественными (мысы, горы, скалы, небольшие островки) или искусственными, специально созданными для целей судовождения (маяки, башни, створные знаки). Ориентирами являются не только объекты на земной поверхности, но также искусственные спутники Земли и небесные светила.

Определение места судна по известным координатам ориентиров является геометрической задачей. Для ее решения используются различные геометрические величины, связывающие координаты ориентиров с координатами точек на земной поверхности. Эти величины называют навигационными параметрами. Примеры навигационных параметров: пеленг на ориентир или обратный пеленг, дистанция до ориентира, вертикальный угол, горизонтальный угол между двумя ориентирами, высота светила, разность расстояний до двух ориентиров и т.д.

Аналитическая зависимость навигационного параметра от координат на земной поверхности называют навигационной функцией U.

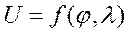
где U − значение параметра; φ и λ − координаты судна

Для получения значений навигационного параметра созданы приборы и системы, с помощью которых измеряются различные физические величины, определенным образом зависящие от взаимного расположения ориентира и судна. Для этого могут использоваться электромагнитные, акустические, геомагнитные, гравитационные поля. При этом измеряются: направление лучей, частоты, фазы и амплитуды радиосигналов, интервалы времени распространения сигналов или их разность и т.п.

Рассмотрим навигационные функции основных навигационных параметров.

Дистанция на плоскости

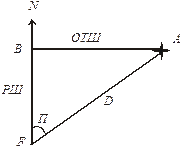
На небольших расстояниях земную поверхность можно принять за плоскую. На рис. 5.1 показаны ориентир А и судно F. Дистанцию D можно определить по теореме Пифагора, где катетами служат разность широт и отшествие:

.

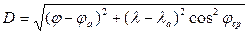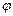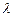где и − координаты судна;

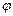_а и 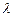_а − координаты ориентира;

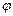_ср − средняя широта между судном и ориентиром.

Рис. 5.1. Пеленг и дистанция

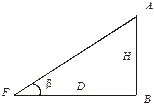
Рис. 5.2. Вертикальный угол на плоскости

Пеленг на плоскости

Из треугольника АВF (рис. 5.1)

.

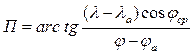Вертикальный угол

Если измерен вертикальный угол какого-либо ориентира, высота которого Н известна (например, маяка или башни), то из треугольника АВF (рис. 5.2) можно найти катет ВF − дистанцию до ориентира

.

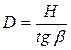Подставив сюда выражение для дистанции из, получим

.

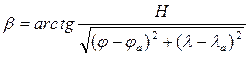Дистанция на сфере

В разделе 2 была получена формула, с помощью которой рассчитывается расстояние между двумя точками на сфере (длина дуги большого круга). Приняв точку В за ориентир, а точку А за место судна, получим навигационную функцию для дистанции на сфере

Пеленг на сфере

В том же разделе получена формула (2.11) для начального курса плавания по ортодромии. Так как эта формула показывает связь между координатами двух точек с направлением из одной точки на другую, то приняв точку В за ориентир, а точку А за место судна, получим навигационную функцию для пеленга на сфере

.

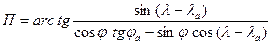Высота светила

Для нахождения навигационной функции высоты светила воспользуемся формулой. Эта формула показывает зависимость высоты светила от координат светила, часового угла t и склонения δ, а также широты места судна φ. В свою очередь часовой угол является алгебраической суммой гринвичского часового угла и долготы места судна.

С учетом этого формулу (2.13) можно записать в виде

.

5.3. Изолинии навигационных параметров

При перемещении по земной поверхности, т.е при изменении φ и λ в формулах −, значение навигационного параметра будет меняться. Однако на земной поверхности существуют точки, в которых значение навигационного параметра остается постоянным. Например, дистанция при перемещении по окружности вокруг ориентира не меняется, пеленг при перемещении по линии FA (рис. 5.1) также не меняется. Для любого навигационного параметра можно найти такие точки.

Геометрическое место точек на земной поверхности, в которых значение навигационного параметра остается постоянным, называется изолинией.

В общем виде уравнение изолинии можно записать так:

.

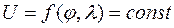Приравняв к константе левые части уравнений −, получим выражения для изолиний конкретных навигационных параметров. Геометрически изолинии могут быть прямыми, кривыми второго порядка на плоскости или сфере.

Основные изолинии, использующиеся в судовождении, имеют собственные названия. Так, например, изолиния расстояния называется изостадией, изолиния пеленга − изопеленгой, изолиния горизонтального угла − изогоной, изолиния высоты светила − кругом равных высот, изолиния разности расстояний − гиперболой (на больших расстояниях − сферической гиперболой).

В пределах изменения навигационного параметра константа в может быть любой и каждой константе соответствует своя изолиния. Подставляя, например, в D = 1 кбт, 2 кбт, 3 кбт и т.д., получим семейство изостадий. Подставляя в значения h = 70^о, 60^о, 50^о и т. д., получим семейство кругов равных высот. На земной поверхности таким семействам соответствуют сетки изолиний.

Понятие изолинии является важнейшим в теории определения места судна, так как измерение навигационного параметра с помощью того или иного прибора позволяет записать конкретное уравнение изолинии, проходящей через место судна. Одно уравнение имеет 2 неизвестных (φ и λ) и не позволяет определить место судна, но измерение второго навигационного параметра дает возможность составить систему двух уравнений с двумя неизвестными, которая в принципе решается и определяет обсервованное место судна.

Использование изолиний в навигации

Основное назначение изолинии − определение места судна. Как уже говорилось, одна изолиния не дает обсервованное место. Для его получения необходимо, как минимум, иметь две изолинии, т.е. следует, по крайней мере, измерить два навигационных параметра. Два навигационных параметра позволяют составить систему двух уравнений вида −, которая решается относительно φ и λ.

Заметим, что прежде, чем подставлять значения измеренных навигационных параметров в уравнения, они должны быть освобождены от всех систематических погрешностей путем введения различных поправок.

Кроме своей основной функции − для определения места судна, изолинии могут служить для ограждения каких-либо опасностей или для задания нужного направления. Так, например, изостадия вокруг какого-нибудь ориентира может ограничить акваторию с несколькими банками, рифами. Две изопеленги маяка могут образовать сектор с аналогичной акваторией. Обычно в таком секторе огонь маяка имеет красный цвет.

Одна изопеленга может использоваться для указания нужного направления при следовании судна каналом или фарватером. Для этого оборудуются специальные створные знаки.

Заранее построенные на карте сетки изолиний позволяют в условиях дефицита времени контролировать местоположение судна без нанесения точки на карту. Измеряя навигационный параметр и сравнивая его со значениями на изолиниях, можно ориентировочно судить о местоположении судна.

Широкое распространение сетки изолиний получили во второй половине ХХ века с внедрением на судах гиперболических радионавигационных систем. Было выпущено большое количество карт с нанесенными на них сетками гипербол − изолиний разности расстояний. При определении места судна с помощью таких сеток гипербола, соответствующая измеренному навигационному параметру, заменялась отрезком прямой и графически интерполировалась между нанесенными изолиниями.

Сетки изолиний использовались ранее и в мореходной астрономии в виде астрографиков.

Особо следует сказать о контрольной функции изолинии в поворотных точках маршрута. Обычно на картах в поворотных точках наносятся контрольные изолинии пеленга или дистанции. Поворот выполняется, как только измеренный навигационный параметр принимает отмеченное на карте значение.

На экране современных РЛС изображается касательная к ограждающей изостадии (так называемая параллельная индексация), которая позволяет заранее увидеть прохождение судном опасного участка и скорректировать в случае необходимости курс судна.

5.4. Обобщенный метод линий положения

Определение места судна по изолиниям имеет существенные недостатки. Графическое решение возможно только для простых изолиний − окружностей и прямых линий. К тому же, если ориентир находится за рамкой карты, такое построение невозможно или требует дополнительных вычислений.

Аналитическое решение тоже затруднено, так как многие изолинии описываются трансцендентными уравнениями (решение которых не выражается алгебраическими корнями). Система трансцендентных уравнений обычно решается методом итераций. В редких случаях можно получить аналитическое решение путем сложных преобразований самих уравнений.

Кроме того, любые две изолинии (кроме прямых) дают более одной точки пересечения. Для устранения неоднозначности решения необходимо привлекать дополнительную информацию. Обычно такой информацией являются координаты счислимой точки.

Указанных недостатков можно избежать, если определять место судна обобщенным методом линий положения, который был предложен В.В.Каврайским в 1920 году. Суть метода заключается в том, что отрезки изолиний в окрестности счислимой точки заменяются касательными. Такая касательная к изолинии вблизи счислимой точки называется линией положения.

Касательная − это прямая независимо от формы изолинии. Поэтому метод называется обобщенным. Две прямые пересекаются в одной точке, что делает решение однозначным. Линия положения строится относительно счислимой точки независимо от того, находится ориентир на карте или нет. Значительно упрощается также аналитическое решение, которое сводится к решению унифицированной системы двух линейных уравнений с двумя неизвестными.

Чтобы получить уравнение касательной к изолинии, надо навигационную функцию разложить в ряд Тейлора, ограничившись линейными членами разложения:

.

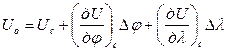Здесь индекс «о» означает обсервованное (измеренное) значение, индекс «с» − счислимое значение.

Уравнение представляет собой уравнение прямой в системе координат, осями которой являются меридиан и параллель, а начало отсчета находится в счислимой точке. Чтобы уравнять масштабы по осям этой системы, надо разность долгот перевести в отшествие, для чего последнее слагаемое в умножим и разделим на cos φ_с. С учетом этого формулу можно представить в виде

,

где 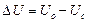− разность значений навигационного параметра в обсервованной и счислимой точке,

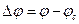− разность широт между обсервованной и счислимой точками,

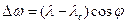− отшествие между обсервованной и счислимой точками.

Физический смысл частных производных следующий:

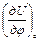− скорость изменения навигационного параметра вдоль меридиана,

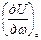− скорость изменения навигационного параметра вдоль параллели,

Для двух навигационных параметров можно составить систему двух уравнений линий положения

,

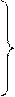
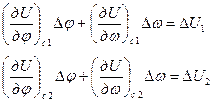которая решается относительно Δφ и Δω. Затем рассчитываются обсервованные координаты:

.

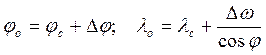Обобщенный метод линий положения имеет некоторые принципиальные отличия от метода изолиний. Во-первых, используются счислимые координаты в навигационных функциях, а не обсервованные. Во-вторых, применение касательных вместо изолиний вносит методическую погрешность в обсервованные координаты, так как действительное место на пересечении изолиний, а не касательных. Однако этими погрешностями при невязках менее 30 миль можно пренебречь. В-третьих, определяются не сами координаты, а их приращения к счислимым.

5.5. Градиент навигационного параметра

Уравнения линии положения в виде можно использовать в аналитическом решении. Однако для построения линии положения на карте от счислимой точки необходимо знать, на сколько должна сместиться линия положения (или изолиния) при изменении навигационного параметра на Δ U.

Это смещение обозначим буквой р. Оно пропорционально изменению навигационного параметра, а коэффициент пропорциональности g называется градиентом навигационного параметра:

Δ U = g р.

Отсюда выразим градиент

.

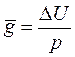При перемещении точки по земной поверхности значение навигационного параметра в ней изменяется по-разному, а вдоль изолинии − вообще не меняется. Максимального значения изменение навигационного параметра достигает при перемещении точки перпендикулярно к изолинии. Поэтому градиентом навигационного параметра называется векторная величина, характеризующая скорость изменения навигационного параметра при перемещении по нормали к изолинии в сторону увеличения параметра.

На рис. 5.3 показана изолиния, проходящая через счислимую точку С и градиент 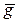, проходящий перпендикулярно к ней.

Как любая векторная величина, градиент характеризуется модулем g и направлением τ. Разложим 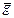по осям и обозначим проекцию градиента на меридиан g _φ, а проекцию на параллель − g _ω. Как видно из рис. 5.3, если 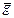характеризует скорость изменения параметра по нормали к изолинии, то g _φ характеризует скорость изменения параметра вдоль меридиана, т.е.

.

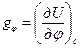Соответственно g _ω характеризует скорость изменения навигационного параметра при перемещении по параллели:

.

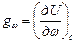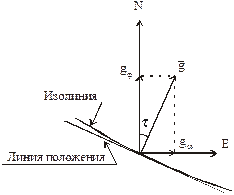
Рис. 5.3. Градиент навигационного параметра

Из построений на рис. 5.3 следует, что

.

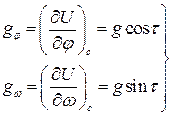Формулы позволяют определять как модуль градиента навигационного параметра, так и его направление через частные производные навигационной функции. Возведя в квадрат каждое уравнение и сложив, найдем квадрат модуля, откуда, извлекая квадратный корень, получим

.

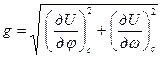Поделив второе уравнение на первое, найдем тангенс направления градиента

.

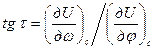По формулам и можно вычислить модуль и направление градиента любого навигационного параметра, если известна его навигационная функция.

Расстояние. Приращение расстояния DD обусловливает такое же смещение Dр изолинии и поэтому модуль градиента расстояния g_D = 1. Направлен этот градиент от ориентира, т.е. t = П +180 °. (С - судно, А – мыс).

Высота светила. Приращение высоты Dh вызывает такое же уменьшение зенитного расстояния Z, которое равно расстоянию до полюса освещения. Поэтому модуль градиента высоты светила такой же, как и расстояния: g_h = 1, а направлен градиент к светилу, т.е. t = А, где А – азимут светила.

Пеленг на плоскости. На рис. 5.4 показано смещение места р при изменении пеленга на Δ П, градиент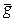направлен в сторону возрастания пеленга, место судна обозначено буквой С, ориентир − А.

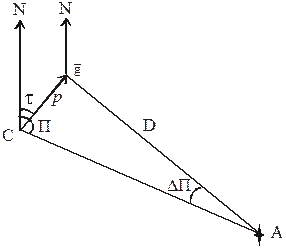
Рис. 5.4. Градиент пеленга на плоскости

Модуль градиента определяется формулой. В данном случае Δ U = Δ П. Из треугольника 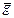СА: р = D sin Δ П или (по малости угла Δ П) р = D Δ П. Подставив в выражения Δ U и р, получим

.

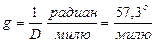Из рис. 5.4 следует: τ = П − 90^о.

5.6. Определение места судна обобщенным методом линий положения

Ранее было получено уравнение линии положения в частных производных. Выразим в нем частные производные через модуль градиента и его направление по формулам:

Δφ g cos τ + Δω g sin τ = ΔU.

Заменив Δ U по формуле и сократив обе части равенства на g, получим уравнение линии положения в нормальном виде

Δφ cos τ + Δω sin τ = р,

где р рассчитывается на основании формулы:

.

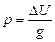Перенос р и его направление τ называются элементами линии положения.

Уравнение линии положения в нормальном виде удобно как для аналитического, так и для графического определения места судна. При аналитическом решении составляется система, как минимум, двух уравнений, которая решается относительно Δφ и Δω, откуда находятся обсервованные координаты.

При графическом решении сначала рассчитываются элементы линии положения. Затем на карте или планшете по направлению τ откладывается от счислимой точки перенос и получают так называемую определяющую точку, через которую перпендикулярно переносу строится линия положения.

Чтобы выяснить последовательность действий при определении места судна обобщенным методом линий положения, раскроем в формуле сокращения:

.

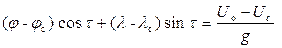Здесь φ и λ − текущие координаты судна, φ_с и λ_с − счислимые координаты на момент обсервации, U _о − измеренное значение навигационного параметра, U _с − значение навигационного параметра в счислимой точке.

Последовательность действий при определении места судна по линиям положения следующая.

1. Измеряются, как минимум, два навигационных параметра.

2. В момент измерения фиксируется время и на этот момент с карты снимаются счислимые координаты.

3. В навигационные функции подставляются счислимые координаты и рассчитываются счислимые навигационные параметры U _{с 1} и U _{с 2}.

4. Рассчитываются или выбираются из справочной литературы модули и направления градиентов навигационных параметров g ₁, τ_1, g ₂, τ₂.

5. Рассчитываются переносы р ₁ и р ₂.

6. Дальнейшее решение может быть выполнено двумя способами − аналитически и графически.

Аналитическое решение задачи определения места судна

Составляется система уравнений линий положения.

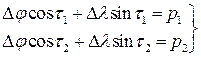
Система решается методом определителей.

D = cos τ₁ sin τ₂ − sin τ₁ cos τ₂ ,

D_Δφ = р₁ sin τ₂ − р₂ sin τ₁ , D_Δω = р₂ cos τ₁ − р₁ cos τ₂ .

.

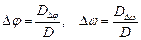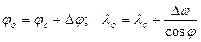
Графическое решение задачи определения места судна

На карте в счислимой точке С проводятся направления τ₁ и τ₂. По этим направлениям откладываются переносы р ₁ и р ₂. Таким образом получаются определяющие точки к ₁ и к ₂. Через эти точки проводятся линии положения перпендикулярно к направлениям градиентов. Пересечение линий положения дает обсервованную точку, координаты которой снимаются с рамок карты.

При построениях следует иметь в виду, что положительные переносы откладываются по направлению градиента, а отрицательные − в обратную сторону.

Описанное графическое решение применяется в мореходной астрономии.

Обобщенный метод линий положения лежит в основе обработки всех навигационных параметров при определении места судна техническими средствами навигации, в которых реализуется, в отличие от рассмотренного, случай избыточных линий положения.

В заключение заметим, что указанный ранее недостаток метода (погрешность от замены изолиний касательными) может быть практически устранен путем решения задачи во втором приближении. Во втором приближении найденные координаты принимаются за счислимые, и задача решается снова.

ТЕМА 6. Оценка точности места судна

6. А

6. Б

6.1. Оценка точности обсервации по двум независимым линиям положения

Ранее было рассмотрено определение места судна с помощью изолиний или линий положения по измеренным навигационным параметрам. Если повторяющаяся часть полной погрешности в измеренном навигационных параметрах пренебрежимо мала по сравнению со случайной частью, линии положения считаются независимыми.

Точность обсервованного места зависит от точности измеренного навигационного параметра. Для выяснения этой зависимости выполним графическое построение линий положения, но уже с учетом погрешностей в навигационных параметрах. На рис. 6.1 показана счислимая точка С, обсервованная точка F и две линии положення, которые проходят через определяющие точки к ₁ и к ₂. Переносы, с помощью которых получены линии положения, имеют случайные погрешности, которые оцениваются СКП − т _лп1 и т _{лп 2}. Это означает, что изображенные на рисунке линии положения являются наиболее вероятными, но могут проходить и в другом месте. Кривые нормального закона распределения также показаны на рисунке. Обсервованная точка получена на пересечении наиболее вероятных линий положения, но в действительности может быть и в другом месте.

СКП линии положения показывает, в каких пределах заключено 68% всех возможных ее положений. Область таких вероятных мест на рис. 6.1 показана пунктиром. Действительная линия положения может проходить и вне этой области, но с вероятностью 32%.

Таким образом, можно утверждать, что с вероятностью 68% судно находится где-то в полосе р ± т _лп. Эта область называется полосой положения. Судоводитель должен полагать, что место судна не на линии, а в полосе положения, притом с вероятностью 68%.

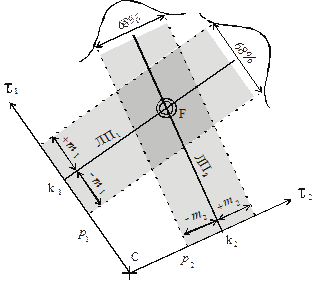
Рис. 6.1. Полосы положения

На пересечении линий положения находится наиболее вероятное место, при этом действительное место судна находится не в этой точке, а в некоторой области около нее.

Пересечение полос положения образует четырехугольник, который называется фигурой погрешностей. Она показывает область, в которой с некоторой вероятностью может находиться действительное место судна.

Вероятность того, что действительное место судна находится в этом четырехугольнике, равна произведению вероятностей полос положения, т.е. 0,68² ≈ 0,46 = 46%. Любая обсервация по двум линиям положения имеет свой четырехугольник погрешностей, площадь которого зависит от ширины полос, т.е. от т _{лп 1} и т _{лп 2}. Чем больше СКП линий положения, тем больше площадь разброса вероятных мест судна, но вероятность нахождения внутри каждой такой фигуры одна и та же − 46%. Это дает возможность по величине фигуры погрешностей судить о точности обсервации.

6.2. Влияние систематической погрешности в линиях положения на обсервованное место

Ранее было рассмотрено определение места судна в предположении о наличии в полной погрешности линии положения случайной составляющей и пренебрежимо малой повторяющейся части. Теперь рассмотрим задачу обсервации, когда повторяющаяся часть полной погрешности явно преобладает над случайной. В таком случае говорят о наличии только систематической погрешности в линии положения.

Допустим, место судна определялось по двум однородным навигационным параметрам. Предположим вначале, что навигационные параметры безошибочны, а линии положения ЛП₁ и ЛП₂, пересекаясь, дают обсервованную точку F, как показано на рис. 6.2.

Если в обоих навигационных параметрах присутствует систематическая погрешность +Δ, она увеличивает переносы пропорционально градиентам на величины

.

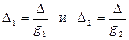Обе линии сместятся по направлению градиентов на Δ₁ и Δ₂ и дадут новую точку пересечения F ₁.

Рис. 6.2. Смещение места судна от систематической погрешности

Если систематическая погрешность Δ₂ будет с обратным знаком, линии положения дадут точку пересечения F ₂ с другой стороны от истинного места F.

Как нетрудно убедиться из построений на рис. 6.2 все точки пересечения лежат на одной прямой, которая называется линией смещения.

Угол ψ между линией смещения и второй линией положения можно получить, рассматривая зависимости сторон в треугольниках на рис. 6.2. Этот угол равен

,

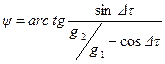где Δτ − угол между направлениями градиентов.

В формуле нет смещений Δ₁ и Δ₂ , т.е. положение линии смещения не зависит от величины и знака систематической погрешности в навигационном параметре, и место судна всегда будет располагаться на этой прямой.

Если градиенты параметров одинаковы (например, для высот светил), выражение упрощается:

.

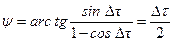Это означает, что линия смещения пойдет по биссектрисе угла между градиентами, которая называется астрономической биссектрисой.

Следует особо отметить, что смещается обсервованная точка именно по биссектрисе угла между градиентами, а не острого угла θ между линиями положения, как может показаться на первый взгляд. Чтобы убедиться в этом, рассмотрим рис. 6.3.

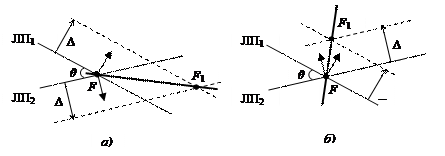
Рис. 6.3. Астрономическая биссектриса

На нем показаны две одинаковые высотные линии положения, смещенные под действием систематической погрешности Δ. Но на рис. 6.3 б) градиент второй высоты светила имеет противоположное направление. Таким образом, при наличии систематической погрешности в линиях положения место судна определить нельзя, а только линию смещения, на которой оно находится, в частном случае на астрономической биссектрисе.

Уравнения двух линий положения, в которых присутствует систематическая погрешность Δ, выглядит следующим образом:

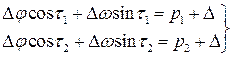
Чтобы избавиться от систематической погрешности, вычтем из первого уравнения второе:

Δφ (cos τ ₁ − cos τ ₂) + Δω (sin τ ₁ − sin τ ₂ ) = р ₁ − р ₂ .

Формула является уравнением астрономической биссектрисы между первой и второй линиями положения. В этом уравнении два неизвестных Δφ и Δω. Чтобы определить место судна нужно уравнение второй биссектрисы. Для этого нужна третья линия положения, которая позволит записать уравнение второй биссектрисы:

Δφ (cos τ ₁ − cos τ ₃) + Δω (sin τ ₁ − sin τ ₃ ) = р ₁ − р ₃ .

Система уравнений и свободна от систематической погрешности и решается, как обычно, относительно Δφ и Δω. Подставив эти значения в уравнение любой линии положения, можно найти и систематическую погрешность Δ. Идентичное решение будет, если вместо записать разностное уравнение второй и третьей линии положения. Третья биссектриса с неизбежностью пройдет через обсервованную точку. Заметим, что третья линия положения не будет избыточной, так как определяются три неизвестных: Δ, Δφ и Δω.

Описанный прием исключения систематической погрешности в линиях положения в графическом варианте путем построения биссектрис используется в мореходной астрономии.

6.3. Эллипс погрешностей

Естественной границей площади, ограничивающей область вероятных мест судна, на первый взгляд кажутся границы полос положения, как это видно на рис. 6.1. Однако более правильным будет проводить границу там, где вероятность местонахождения одна и та же. Наибольшая вероятность в обсервованной точке, и чем дальше от нее, тем меньше эта вероятность.

Чтобы выяснить геометрическую фигуру границы, проходящей через точки равной вероятности, обратимся к рис. 6.4. На нем показана обсервованная точка F и два направления градиентов навигационных параметров, по которым определялось место судна. Вдоль этих направлений действуют случайные погрешности, распределенные по нормальному закону.

Допустим, что действительное место судна находится в точке Z, т.е. была допущена погрешность в первой линии положения х, а во второй − у.

Вероятность того, что будут одновременно допущены погрешности х и у, равна произведению их вероятностей. Геометрически двумерная плотность вероятности представляет собой холмообразную поверхность, показанную на рис. 6.4.

Запишем условие постоянства плотности распределения, заменив в формуле (5.22) средние квадратические отклонения на средние квадратические погрешности, а отклонения от математического ожидания на погрешности х и у:

.

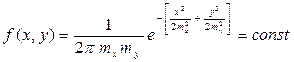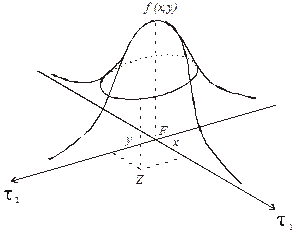
Рис. 6.4. Плотность распределения погрешностей в линиях положения

Геометрически это соответствует сечению поверхности горизонтальной плоскостью.

В формуле переменным является только показатель степени е. Чтобы выполнить условие, надо приравнять показатель константе. Выберем константой величину − с ²/2:

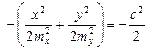
или

.

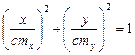Это выражение является уравнением эллипса с полуосями ст_х и ст_у.

Таким образом, площадь разброса вероятных мест судна должна ограничиваться эллипсом, который называется эллипсом погрешностей.

Задаваясь различным значением коэффициента кратности с перед СКП линий положения, получим семейство эллипсов с центром в обсервованной точке. Если с = 1, эллипс называется средним эллипсом погрешностей, при с = 2 эллипс называется двойным, при с = 3 эллипс называется тройным или предельным.

Вероятность того, что действительное место судно находится внутри эллипса погрешностей, определяется двойным интегрированием в некоторой области D выражения

.

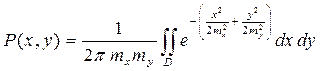Решение имеет вид

.

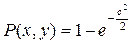Подставляя в значения с = 1, 2, 3, получим вероятности нахождения судна в среднем, двойном и тройном эллипсе погрешностей, которые представлены в таблице 6.1.

Таблица 6.1 Вероятности нахождения судна в различных эллипсах

с		1,5		2,5
	Р	0,393	0,675	0,865	0,956	0,989

Как видно из таблицы, вероятность того, что судно находится внутри среднего эллипса составляет около 39%. Такая вероятность явно недостаточна. По требованиям Международной морской организации (ИМО), регламентирующей стандарты судовождения, любая фигура погрешностей должна накрывать действительное место судна с вероятностью 95%. Для такого эллипса коэффициент с должен быть равен 2,5. Это означает, что для получения 95% вероятности полуоси среднего эллипса надо увеличить в 2,5 раза.

Оценка точности обсервации эллипсом погрешностей

Дата добавления: 2014-01-11