Координаты центра окружности можно вычислить, решив, например, линейную засечку с пунктов A и B на точку C

Если подставить в уравнение (5.3) значения X_C, Y_C и R, то получится сложное уравнение второй степени относительно неизвестных X и Y. Из одного уравнения два неизвестных найти невозможно, следовательно, измерения одного угла β на определяемой точке недостаточно для определения двух координат этой точки.

Рис. 5.4 – Третье элементарное измерение

Для однозначного определения двух координат точки P нужно выполнить измерение двух элементов. Количество комбинаций из трёх по два равно шести; комбинации двух элементарных измерений для определения координат одной точки называются геодезическими засечками.

1. Измеряются один угол и одно расстояние; оба измерения выполняются на пункте A, – полярная засечка;

2. Измеряются два угла; один угол измеряется на пункте A, другой - на пункте B, - прямая угловая засечка;

3. Измеряются два расстояния; одно расстояние - от пункта A до пункта P, другое – от пункта B до пункта P, - линейная засечка;

4. Измеряются два угла; оба измерения выполняются на точке P; один угол − между направлениями на исходные пункты A и B, другой – между направлениями на исходные пункты B и D, - обратная угловая засечка.

Пятая и шестая комбинации названий не имеют и для определения координат точки P не применяются.

Полярная засечка

В полярной засечке исходными данными являются координаты пункта А и дирекционный угол 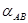направления АВ (если дирекционный угол 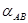не задан, нужно решить обратную геодезическую задачу между пунктами А и В и вычислить его); измеряемыми данными являются горизонтальный угол 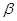(средняя квадратическая ошибка измерения угла 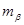) и расстояние 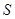(относительная ошибка измерения расстояния 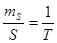); определяемые данные – координаты точки P.

Графическое решение.

Сначала на чертеже (плане) нужно построить систему координат и нанести точки Α и Β по их известным координатам; затем нужно соединить точки Α и Β прямой линией, от линии ΑΒ отложить по часовой стрелке угол β и провести линию положения точки P. Зафиксировать на циркуле расстояние S в масштабе чертежа (плана) и провести небольшую дугу радиусом S; точка пересечения линии и дуги является искомой точкой P (рис.5.5).

Рис.5.5 – Схема полярной засечки

Аналитическое решение.

Вычислим дирекционный угол направления АP и запишем два уравнения, соответствующие двум элементарным измерениям: уравнение прямой линии, проходящей через точку А в заданном направлении АP, и уравнение окружности радиусом 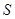с центром в точке А

Алгоритм решения полярной засечки в кратком виде:

- вычислить дирекционный угол линии AP ;

- вычислить приращения координат: ; ;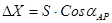

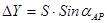- вычислить координаты точки P: ; ;

Прямая и обратная геодезические задачи

Прямая геодезическая задача - это вычисление координат , 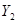второго пункта, если известны координаты , 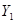первого пункта, дирекционный угол и длина 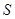линии, соединяющей эти пункты.

Прямая геодезическая задача является частью полярной засечки, и формулы для ее решения берутся из набора формул для решения полярной засечки

,

. (5.5)

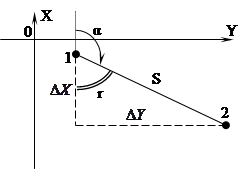Обратная геодезическая задача - это вычисление дирекционного угла и длины 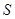линии, соединяющей два пункта с известными координатами и 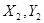(рис.5.6).

Рис.5.6 – Схема обратной геодезической задачи

Построим на отрезке 1-2 как на гипотенузе прямоугольный треугольник с катетами, параллельными осям координат. В этом треугольнике гипотенуза равна 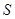; катеты равны приращениям координат точек 1 и 2 ( ), а один из острых углов равен румбу линии 1-2.

Если и 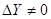, то треугольник решается по известным формулам

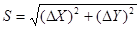; (5.6)

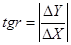и 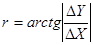. (5.7)

Для данного рисунка направление линии 1-2 находится во второй четверти, поэтому

. (5.8)

Общий порядок нахождения дирекционного угла линии 1-2 включает две операции:

- определение номера четверти по знакам приращений координат ;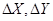

- вычисление дирекционного угла по формулам связи дирекционного угла и румба в соответствии с номером четверти.

Контролем правильности вычислений является выполнение равенства

. (5.9)

Если 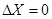, то ,

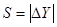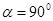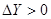при ;

при .

Если , то ,

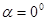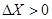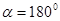при ;

при .

Для решения обратной задачи в автоматическом режиме (в программах для ЭВМ) используется другой алгоритм, не содержащий тангенса угла и исключающий возможное деление на ноль при :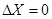

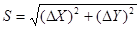, (5.10)

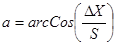, (5.11)

если , то ; (5.12)

если , то 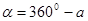. (5.13)

Прямая угловая засечка

Сначала рассмотрим так называемый общий случай прямой угловой засечки (сокращённо ПУЗ), когда углы и 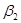измеряются на двух пунктах с извест­ными координатами, каждый от своего направления с известным дирекционным углом (рис.5.6).

Исходные данные: ;

Измеряемые элементы: ;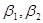

Неизвестные элементы: точки .

Если или 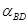не заданы явно, нужно решить обратную геодезическую задачу сначала между пунктами A и C и затем между пунктами B и D.

Графическое решение. От направления AC отложить с помощью транспортира угол и провести прямую линию AP; от направления BD отложить угол 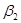и провести прямую линию BP; точка пересече­ния этих прямых является искомой точкой P.

Рис.5.6 – Общий случай прямой угловой засечки Рис.5.7 – Частный случай ПУЗ

Аналитическое решение. Приведем алгоритм, соответ­ствующий общему случаю засечки:

1) вычислить дирекционные углы линий AP () и BP ()

; ;

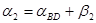2) написать два уравнения прямых линий

для линии АР ,

для линии ВР ;

3) решить систему двух уравнений и вычислить неизвестные коор­динаты

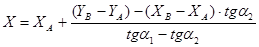, (5.14)

. (5.15)

Частным случаем прямой угловой засечки считают тот случай, когда углы и 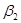измерены от направлений AB и B A, причем угол - правый, а угол 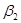- левый (в общем случае засечки оба угла - левые), - рис.31.

Решение прямой угловой засечки методом треугольника соответ­ствует частному случаю засечки. Порядок решения прямой угловой засечки методом треугольника:

1) решить обратную задачу между пунктами A и B и получить дирекционный угол 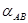и длину 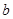линии AB,

2) вычислить угол при вершине P ;

3) используя теорему синусов для треугольника APB

,

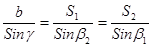вычислить длины сторон AP ()и BP ();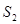

4) вычислить дирекционные углы и

, ;

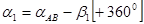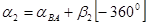5) решить прямую задачу от пункта A к точке P и для контроля - от пункта B к точке P; оба решения должны совпасть.

Для вычисления координат в частном случае прямой угловой засечки можно использовать формулы Юнга

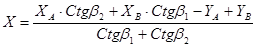, (5.16)

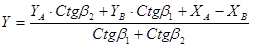. (5.17)

От общего случая прямой угловой засечки нетрудно перейти к частному случаю; для этого нужно сначала решить обратную геоде­зическую задачу между пунктами A и B и получить дирекционный угол 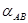линии A B и затем вычислить углы в треугольнике APB при вершинах A и B

и 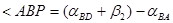. (5.18)

Линейная засечка

В линейной засечке исходными данными являются координаты пунктов А и В; измеряемыми данными являются расстояния и 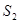(относительная ошибка измерения расстояний 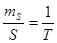); определяемые данные – координаты точки P (рис.5.8).

Рис. 5.8 – Линейная засечка

Графическое решение.

Сначала на чертеже (плане) нужно построить систему координат и нанести точки Α и Β по их известным координатам; затем нужно провести две окружности с центрами в точках Α и Β, первую окружность – радиусом и вторую – радиусом ; одна из точек пересечения этих окружностей и является искомой точкой Р; другая точка P’ является вторым (альтернативным) вариантом решением засечки (рис.5.8)

Аналитическое решение линейной засечки может быть выполнено по двум алгоритмам: первый из них предусматривает решение системы уравнений двух измеренных расстояний

,

.

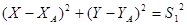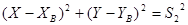Второй алгоритм предусматривает решение треугольника АВР по формулам планиметрии:

- в треугольнике ABР по теореме косинусов вычислить углы β₁ и β₂

,

; (5.19)

- вычислить угол γ этого же треугольника ;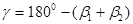

- вычислить дирекционные углы сторон AР и BР:

точка Р справа от линии AB

,

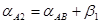; (5.20)

точка Р слева от линии AB

,

; (5.21)

дирекционный угол α_AB следует взять равным углу α из решения обратной геодезической задачи между точками A и B; ;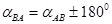

- решить прямые геодезические задачи:

из пункта A на точку P

,

, (5.22)

и из пункта B на точку P

,

; (5.23)

расхождение координат 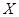и по двум решениям не должно превышать величины, соответствующей точности вычислений.

Обратная угловая засечка

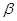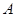К элементарным измерениям относится и измерение угла на определяемой точке между направлениями на два пункта и 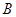с известными координатам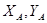и и . Однако, это измерение оказывается теоретически довольно сложным, поэтому рассмотрим его отдельно. Проведем окружность через три точки 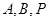. Из школьного курса геометрии известно, что угол с вершиной на окружности измеряется половиной дуги, на которую он опирается. Центральный угол, опирающийся на ту же дугу, измеряется всей дугой, следовательно, он будет равен (рис.5.9).

Расстояние 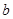между пунктам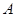и и 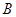считается известным, и из прямоугольного треугольника можно найти радиус окружности

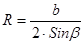. (5.24)

Уравнение окружности имеет вид

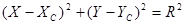, (5.25)

где 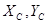- координаты центра окружности. Их можно вычислить, решив либо прямую угловую, либо линейную засечку с пунктов 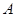и 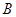на точку 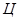. В уравнении (5.25) - координаты любой точки окружности, в том числе и точки , но для нахождения двух координат точки одного такого уравнения недостаточно. Обратной угловой засечкой называют способ определения координат точки по двум углам и , и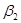змеренным на определяемой точке между направлениями на три пункта с известными координатами (рис.5.10).

Рис.5.9 - К вычислению R и координат Ц Рис.5.10 – Обратная угловая засечка

Исходные данные: ;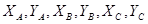

Измеряемые элементы: ;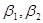

Неизвестные элементы: координаты точки - .

Графическое решение. Приведем способ Болотова графического решения обратной угловой засечки. На листе прозрачной бумаги (кальки) нужно построить углы и 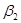с общей вершиной ; затем наложить кальку на чертеж и, перемещая ее, добиться, чтобы направления углов на кальке проходили через пункты на чертеже; переколоть точку с кальки на чертеж.

Аналитическое решение. Аналитическое решение обратной угловой засечки предусматривает ее разложение на более простые задачи, например, на две прямые угловые засечки и одну линейную, или на три линейных засечки и т.д. Известно более десяти способов аналитического решения, но мы рассмотрим только один - через последовательное решение трех линейных засечек. Предположим, что положение точки известно, и проведем две окружности: одну радиусом через точки 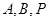и другую - радиусом 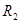через точки 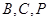(рис.5.10). Радиусы этих окружностей получим по формуле (5.24)

; .

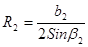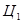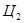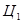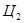Если координаты центров окружностей (точек и ) будут известны, то координаты точки можно определить по формулам линейной засечки: из точки по расстоянию и из точки - по расстоянию 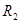. 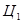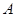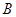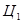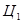Координаты центра можно найти по формулам линейной засечки из точек и по расстояниям , причем из двух решений нужно взять то, которое соответствует величине угла ; если , то точка находится справа от линии ; если , то точка находится слева от линии . 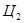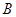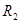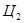Координаты центранаходятся по формулам линейной засечки из точек и по расстояниям , и одно решение из двух возможных выбирается по тому же правилу: если , то точка находится справа от линии 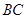, если , то точка 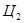находится слева от линии 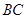. 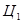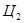Координаты точки находятся из решения линейной засечки с точек (расстояние ) и (расстояние ).

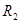Задача не имеет решения, если все четыре точки и находятся на одной окружности, так как обе окружности сливаются в одну, и точку их пересечения указать невозможно.

3.2.8. Комбинированные засечки

В рассмотренных способах решения засечек количество измерений принималось теоретически минимальным (два измерения), обеспечивающим получение результата, однако, при этом нет контроля правильности измерений. На практике для нахождения координат 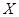и одной точки, как правило, выполняют не два, а три и более измерений; понятно, что в этом случае появляется возможность контроля измерений, и, кроме того, повышается точность решения задачи. Каждое измерение, вводимое в задачу сверх теоретически минимального количества, называют избыточным; оно порождает одно дополнительное решение. Геодезические засечки без избыточных измерений принято называть однократными, а засечки с избыточными измерениями - многократными.

При наличии избыточных измерений вычисление неизвестных выполняют по способу уравнивания. В настоящее время алгоритмы строгого уравнивания измерений в различных геодезических построениях реализованы в машинных программах на ЭВМ; для ручного счета обычно применяют нестрогие (упрощенные) способы уравнивания. Упрощенный способ уравнивания какой-либо многократной засечки (измерений) предусматривает сначала формирование и решение всех возможных вариантов независимых однократных засечек (их число равно 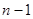), а затем - вычисление средних значений координат точки из всех полученных результатов, если они различаются между собой на допустимую величину.

Для оценки точности однократных засечек существуют следующие формулы:

- для полярной засечки: 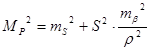; (5.26)

- для прямой угловой засечки: ; (5.27)

- для линейной засечки: 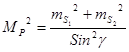. (5.28)

- При оценке точности обратной угловой засечки правая часть формулы ошибки положения точки должна содержать три слагаемых:

- за ошибку линейной засечки точки 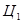с исходных пунктов 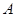и ,

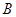- за ошибку линейной засечки точки 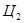с исходных пунктов 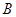и ,

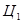- за ошибку линейной засечки точки с точек и .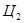

ЛЕКЦИЯ 6. КЛАССИФИКАЦИЯ ЛИНЕЙНО-УГЛОВЫХ ХОДОВ.

ТОЧНЫЕ ИЗМЕРЕНИЯ ГОРИЗОНТАЛЬНЫХ УГЛОВ.

Классификация линейно-угловых ходов.

Определение линейно-углового хода можно дать как с позиций геометрии (линейно-угловой ход – это ломаная линия, в которой измеряют длины сторон и углы между ними), так и с позиций метода определения координат пунктов хода (линейно-угловой ход – это последовательность полярных засечек); оба определения являются верными и дополняют одно другое. Классификацию линейно-угловых ходов можно провести по двум параметрам – по геометрическим характеристикам хода и по точности выполняемых в ходе измерений.

В зависимости от формы хода различают:

-стандартный разомкнутый линейно-угловой ход (рис.6.1-а);

-разомкнутый ход с частичной или полной координатной привязкой;

-стандартный замкнутый линейно-угловой ход (рис.6.1-б);

-висячий линейно-угловой ход;

-свободный линейно-угловой ход.

Рис.6.1 – Некоторые стандартные формы линейно-угловых ходов

В зависимости от точности измерений углов и расстояний линейно-угловые ходы делятся на две группы – теодолитные ходы и полигонометрические ходы.

Полигонометрические ходы в сетях сгущения бывают 4-го класса, 1-го и 2-го разрядов (табл.6.1).

В государственных геодезических сетях полигонометрические ходы бывают 1-го, 2-го, 3-го и 4-го классов точности; однако, в соответствии с “Основными положениями о государственной геодезической сети РФ” выпуска 2004 года основным способом создания государственных сетей становятся спутниковые измерения, а полигонометрические ходы классной точности могут применяться только в геодезических построениях специального назначения.

Основные характеристики полигонометрических сетей сгущения (согласно Письма ГУГК СССР N: 1-1052 от 11 ноября 1987 года) Таблица 6.1

Показатели	4-й класс	1-й разряд	2-й разряд
Предельная длина в км отдельного хода при измерении линий светодальномерами в зависимости от числа сторон	8 при n = 30 10 при n = 20 12 при n = 15 15 при n = 10 20 при n = 5	10 при n = 50 12 при n = 40 15 при n = 25 20 при n = 15 25 при n = 10	6 при n = 30 8 при n = 20 10 при n = 20 12 при n = 8 14 при n = 6
Предельная длина в км отдельного хода при измерении линий другими методами
Длина стороны хода в км: наименьшая наибольшая	0,25 2,00	0,12 0,80	0,08 0,35
Предельная относительная невязка хода	1:25 000	1:10 000	1:5 000
Средняя квадратическая ошибка измерения угла (по невязкам ходов)	2”	5”	10”
Допустимое значение угловой невязки
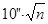
Средняя квадратическая ошибка измерения длины	до 0,5 км – 2 см от 0,5 км до 1 км – 3 см свыше 1 км – 1:40 000	до 1 км – 3 см свыше 1 км – 1:30 000	до 1км – 5 см

Центры геодезических пунктов служат для точного обозначения места пункта и долговременной его сохранности. Центры имеют различную конструкцию; каждая конструкция называется типом центра и имеет своё обозначение, например тип 5 г.р., 6 г.р. и т.д.

Пункты 4-го класса, 1-го и 2-го разрядов закрепляются центрами типа 5 г.р. и 6 г.р. Первый состоит из двух бетонных монолитов в виде усечённой четырёхгранной пирамиды, поставленных один на другой (рис.6.1-а); на верхней грани каждого блока крепится марка; центры марок должны находиться на одной вертикальной линии. Центр типа 6 г.р. представляет собой один бетонный монолит в виде усечённой четырёхгранной пирамиды с заделанной в него металлической трубой; марка центра крепится к верхней части трубы; нижняя часть трубы заделывается в бетон и крепится двумя металлическим стержнями-якорями (рис.6.1-б). Над центром устанавливается чугунный колпак с крышкой и опорными бетонными кольцами или кирпичной кладкой. Центры, закладываемые в стены и фундаменты зданий и сооружений, называются стенными марками; они закладываются на высоте 0,5м – 1,0 м от земной поверхности

Рис. 6.1 –

Устройство, поверки и исследования точных теодолитов

К точным теодолитам относятся теодолиты Т2 и Т5; по ГОСТу 10529-96 предусматривается выпуск теодолитов в двух вариантах: с трубой прямого и обратного изображения. В шифре теодолита на первом месте может стоять цифра 2, 3 или 4 в соответствии с номером модификации теодолита; после цифр точности теодолита могут стоять буквы А, М, К, П. Буква А означает автоколлимационный, буква М – маркшейдерский, буква К – компенсатор вместо уровня при вертикальном круге, буква П – прямое изображение в зрительной трубе.

Некоторые характеристики теодолитов Таблица 6.2

Характеристики теодолитов	T2	3Т2КП	3Т5КП
Увеличение зрительной трубы	25^х	30^х	30^х
Угол поля зрения трубы	1^030’	1^040’	1^040’
Диаметр объектива	40 мм	40 мм	40 мм
Наименьшее расстояние визирования	1,5 м	1,5 м	1,5 м
- с насадкой на объектив	0,9 м	0,9 м	0,9 м
Диаметр лимбов (горизонтального/вертикального)	90/65 мм	90/90 мм	90/ мм
Цена деления лимба λ	20’	20’	1^0
Название отсчётного устройства	Оптический микрометр	Оптический микрометр	Шкаловой микроскоп
Цена деления шкалы отсчётного устройства	1”	1”	1’
Точность отсчитывания	0,1”	0,1”	0,1’
СКО измерения - горизонтального угла	2”	2”	4,5”
- вертикального угла	2”	2”	8”
Диапазон работы компенсатора вертикального круга	3,5’	3,5’	4’
Цена деления уровней: - цилиндр. при алидаде гор. круга	15”	15”	30”
- круглого установочного	5’	5’	5’
Встроенный оптический центрир: - увеличение трубы	2,5^х	2,5^х	2,5^х
- пределы визирования	от 0,8 м	от 0,8 м	от 0,8 м
Масса: - теодолита	4 кг	4 кг	3,7 кг
- подставки	0,7 кг	0,7 кг	0,7 кг

В комплект теодолита для точных измерений углов входят также визирные марки и оптические центриры. Этот комплект заводского изготовления называется КВЦ (комплект визирных целей); он включает 4 визирные марки, 3 подставки, 3 штатива с отвесом, 1 оптический двусторонний центрир ОДО, 1 вешку и некоторые другие мелкие приспособления.

Основным отличием точного теодолита от технического теодолита является использование в качестве отсчётного устройства оптического микрометра с плоскопараллельной пластинкой или с оптическими клиньями.

Нарисуем схему расположения основных частей оптического микрометра с плоскопараллельной пластинкой при взятии отсчёта по лимбу (рис.6.1). Пусть цена деления лимба 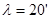, количество делений на шкале микрометра 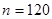, цена одного деления микрометра 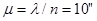, точность отсчитывания 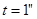; минутные деления на шкале микрометра подписаны.

Рис.6.1 – Схема оптического микрометра с плоскопараллельной пластинкой

В исходном положении лучи света падают на плоскопараллельную пластинку перпендикулярно её граням (то есть, 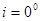); на шкале оптического микрометра стоит отсчёт , так как пластинка занимает нейтральное положение. Отсчётный индекс шкалы лимба (биссектор) находится между штрихами 21⁰ 00’ (младший штрих) и 21⁰ 20’ (старший штрих).Для измерения доли деления лимба от младшего штриха до отсчётного биссектора поворачивают пластинку на некоторый угол . Лучи, идущие от штрихов лимба, смещаются относительно неподвижного биссектора, и, когда изображение штриха 21⁰ совместится с биссектором, вращение пластинки прекращают. При повороте пластинки шкала микрометра двигается, в результате чего на ней против отсчётного индекса шкалы микрометра (одиночный штрих) устанавливается отсчёт, соответствующий углу .

Полный отсчёт по лимбу будет равен .

Теодолит Т2 - оптический теодолит с цилиндрической неповторительной системой вертикальных осей с поворотным горизонтальным лимбом, оптическим микрометром с раздвижными клиньями и оптическим центриром. Прибор устанавливается на подставке, которая прикрепляется к штативу с помощью треугольной металлической пластины и станового винта. Прибор входит во втулку подставки и закрепляется винтом.

В качестве отсчётного приспособления в теодолите Т2 используется оптический микрометр, который имеет две пары оптических клиньев, барабан, шкалу и отсчётный индекс для взятия отсчёта по шкале микрометра. Шкала микрометра разделена на 600 делений, которые проходят около отсчётного индекса за то время, за какое изображения штрихов лимба смещаются на половину деления, то есть, на 10’; таким образом, цена одного деления шкалы микрометра равна 1”.

Конструкция оптического микрометра с двусторонним отсчитыванием включает две пары оптических клиньев; верхние клинья каждой пары - подвижные. В поле зрения такого микрометра видны изображения штрихов диаметрально противоположных частей лимба и в другом окне - деления шкалы микрометра и отсчетный индекс шкалы микрометра – неподвижный штрих (рис.6.2). При вращении барабана микрометра штрихи верхнего и нижнего изображений перемещаются в противоположные стороны, то-есть, совмещение штрихов лимба производится через половину деления лимба, и поэтому длина шкалы микрометра равна половине деления лимба.

Поле зрения отсчётного микроскопа теодолита Т2 показано на рис.6.2; там видно два окошка – большое (оно слева) и малое (оно справа). В левом окошке вверху видно изображение штрихов основной стороны лимба, внизу – изображение штрихов диаметрально противоположной стороны. При вращении барабана микрометра эти изображения двигаются в противоположные стороны. Каждый градус лимба подписан и разделён на три части (цена одного деления шкалы лимба 20’).

Рис.6.2 – Поле зрения оптического микрометра теодолита Т2

Отсчёт по лимбу с помощью оптического микрометра выполняется в следующем порядке:

1. Вращением барабана микрометра тщательно совмещают изображения штрихов верхней и нижней частей левого окошка (если это сделать затруднительно, то совмещают изображения штрихов хотя бы в центре поля зрения);

2. Записывают число градусов по верхнему изображению штрихов; нужный градус располагается слева от центра поля зрения или в самом центре поля зрения и так, чтобы градусный штрих нижнего изображения, отстоящий от него на 180⁰, был справа или точно в центре поля зрения;

3. Считают число двадцатиминутных интервалов между этими двумя штрихами и записывают десятки минут отсчёта, как произведение числа интервалов на 10';

4. В правом окошке напротив неподвижного горизонтального отсчётного индекса отсчитывают по шкале микрометра минуты, секунды и десятые доли секунд, последние оцениваются на глаз (отсчёт на рис.6.2 равен 57⁰ 38’ 00,6”).

Порядок отсчитывания по вертикальному кругу такой же, но перед взятием отсчёта здесь нужно привести пузырёк уровня при вертикальном круге точно в нуль-пункт с помощью микрометренного винта алидады вертикального круга. Формулы для вычисления места зенита и зенитного расстояния имеют вид

, (6.1)

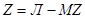, , . (6.2)

В этих формулах через Л и П обозначены отсчёты по вертикальному кругу при круге лево и круге право соответственно.

Поверки точных теодолитов. Теодолит, как прибор для точного измерения горизонтальных и вертикальных углов, должен удовлетворять определённым механико-технологическим и геометрическим условиям.

Главными механико-технологическими условиями являются:

- свободное, плавное и правильное перемещение всех подвижных частей прибора;

- жёсткость и прочность конструкции, обеспечивающие постоянство взаимного расположения его рабочих частей;

- надёжность и устойчивость прибора при полевой эксплуатации, высококачественное изготовление уровней, точное и чёткое нанесение сеток нитей;

- обеспечение заданных параметров зрительной трубы, отсчётной системы и оптического компенсатора;

- высокоточное изготовление и сборка осевых систем;

- точное разделение и нанесение тонких штрихов лимбов, шкал, индексов;

- герметичность конструкции и т.д.

Геометрические условия вытекают из принципа измерения горизонтальных и вертикальных углов; с основными геометрическими условиями теодолитов студенты знакомятся в процессе изучения начального курса геодезии. Перечислим основные геометрические условия теодолита Т2 (рис.6.2):

- Ось цилиндрического уровня UU при алидаде горизонтального круга должна быть перпендикулярна к оси вращения алидады ZZ;

- Визирная ось VV зрительной трубы должна быть перпендикулярна к оси HH вращения трубы;

- Вертикальная нить ss сетки нитей должна лежать в коллимационной плоскости зрительной трубы;

- Ось HH вращения зрительной трубы должна быть перпендикулярна к оси ZZ вращения алидады;

- Место зенита вертикального круга должно быть постоянным и близким к нулю;

- Визирная ось ЦЦ оптического центрира должна совпадать с осью ZZ вращения алидады.

Рис.6.2 – Схема геометрических осей теодолита

Исследование точных теодолитов. Исследования геодезических приборов вообще и теодолитов в частности могут быть общими и текущими. Общие исследования выполняются при получении новых приборов или после капитального ремонта, а также в профилактических целях в межсезонный период. Текущие исследования выполняются ежегодно перед выездом на полевые работы и имеют целью определить:

- неустранимые отклонения от геометрических и оптико-механических условий с целью введения необходимых поправок в результаты измерений;

- постоянные прибора;

- ошибки шкал измерительных приспособлений;

- качество работы отдельных частей и механизмов прибора и прибора в целом.

При проведении текущих исследований проверяют:

- правильность работы оптического микрометра (систематические ошибки оптического микрометра, ошибки совмещения штрихов горизонтального и вертикального кругов, мёртвый ход винта оптического микрометра;

- рен оптического микрометра;

- систематические ошибки измерения углов, связанные с люфтом подъёмных винтов и смещением горизонтального круга;

- эксцентриситет горизонтального круга;

- эксцентриситет алидады горизонтального круга;

- цену деления уровня;

- правильность работы фокусирующей линзы;

- СКО измерения горизонтального угла;

- СКО измерения вертикального угла.

Определение рена отсчетного устройства. Реном называют разность между номинальным значением цены деления лимба (или полуделения лимба) и её значением, измеренным по шкале отсчётного устройства.

У шкалового микроскопа значение рена допускается 0.2 деления шкалы микроскопа; если фактическое значение рена превышает этот предел, теодолит подлежит ремонту в мастерской.

Методика определения рена оптического микрометра зависит от конструкции микрометра. У оптического микрометра с односторонним отсчитыванием подвижной оптической деталью является плоскопараллельная пластинка, и длина шкалы микрометра равна одному делению лимба. Для отсчета по лимбу имеется неподвижный биссектор, а для отсчета по шкале микрометра - неподвижный отсчётный индекс-штрих. Рен такого микрометра определяют по разности отсчетов по микрометру при совмещении с биссектором двух соседних штрихов лимба.

У оптического микрометра с двухсторонним отсчитыванием определяют рен верхнего изображения штрихов лимба и рен нижнего изображения. Измерение расстояния между соседними штрихами верхнего изображения выполняется с помощью одного из штрихов нижнего изображениями, и, наоборот, измерение расстояния между соседними штрихами нижнего изображения выполняется с помощью одного из штрихов верхнего изображения.

Шкала лимба

Шкала микрометра

Рис.6.3 – Схема определения рена оптического микрометра

Сначала устанавливают отсчёт по шкале микрометра 0’00” и точно совмещают штрих A верхнего изображения со штрихом (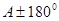) нижнего изображения (рис.6.3) и берут близкий к нулю отсчет a по шкале микрометра со знаком (“плюс” - отсчётный индекс ниже деления 0’00 ”, “минус” - отсчётный индекс выше деления 0’00 ”). Затем вращают барабан оптического микрометра до конца его шкалы и точно совмещают штрих () верхнего изображения со штрихом (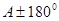) нижнего изображения и берут по шкале микрометра отсчет b со знаком (“плюс” - отсчётный индекс ниже деления 10’00 ”, “минус” - отсчётный индекс выше деления 10’00 ”). Затем точно совмещают штрих A верхнего изображения со штрихом (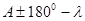) нижнего изображения (эта пара штрихов находится справа от предыдущей пары штрихов – при отсчётё b) и берут отсчет c со знаком.

Рен верхнего изображения вычисляют по формуле 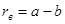, и рен нижнего изображения по формуле .

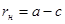При исследовании теодолитов рен оптического микрометра определяют на разных частях лимба, переставляя его через 45⁰20’. Из всех определений вычисляют среднее значение рена 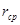и разность ренов

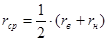и .

Если значение рена превышает 2”, то в каждый отсчет по лимбу вводится поправка за рен

,

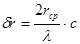где: - отсчет по шкале микрометра в минутах,

- цена деления лимба, .

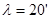При большом значении рена (больше 5 ”) теодолит нужно сдать в мастерскую для юстировки.

Эксцентриситеты горизонтального круга. В плоскости лимба различают три точки: главная точка Д – центр окружности делений лимба, Л – центр вращения лимба (точка пересечения оси вращения лимба с плоскостью лимба), А – центр вращения алидады (точка пересечения оси вращения алидады с плоскостью лимба). В идеале все три точки должны совпадать, но в реальном инструменте они не совпадают: несовпадение точки А с точкой Д называется эксцентриситетом алидады, несовпадение точки Л с точкой Д называется эксцентриситетом лимба, несовпадение точек А и Л называется эксцентриситетом осей. Исследование эксцентриситетов горизонтального круга выполняют по методике, изложенной в Инструкции [8]. Эксцентриситет лимба и эксцентриситет алидады оптических теодолитов исследуют по одной и той же методике, только при определении эксцентриситета алидады переставляют алидаду через 30⁰ от 0⁰ до 330⁰ в прямом и обратном направлениях, а при определении эксцентриситета лимба переставляют лимб через 30⁰ от 0⁰ до 330⁰ также в прямом и обратном направлениях.

При каждой установке лимба сначала совмещают изображения диаметрально противоположных штрихов лимба и берут отсчет t, затем совмещают изображение верхнего штриха с неподвижным индексом в поле зрения отсчётного микроскопа и берут отсчет t’. Изменение разноcти характеризует величину эксцентриситета. При отсутствии неподвижного индекса его роль может выполнять любая неподвижная точка в поле зрения оптического микрометра. По данным исследования строят график изменения величины и проводят на нем плавную кривую типа синусоиды; отклонение точек графика от синусоиды не должно быть больше 15".

Затем вычисляют эксцентриситет осей и максимальный эксцентриситет, значение которого не должно превышать 40". В теодолитах с двусторонним отсчитыванием (именно к таким теодолитам относятся теодолиты серий Т2) влияние эксцентриситета на отсчёт по лимбу исключается, однако значительная его величина может привести к изменению рена на разных частях круга, поэтому предельное значение эксцентриситета инструкцией ограничено.

В теодолитах с односторонним отсчитыванием (типа Т5) каждый отсчёт по лимбу искажён на величину эксцентриситета, поэтому методика измерений разрабатывается так, чтобы исключить влияние эксцентриситета.

3.3.2.3. Методика точного измерения горизонтальных и вертикальных углов

При точных измерениях горизонтальных углов применяют, как правило, способ круговых приемов; этим способом измеряют углы на пунктах, где имеется больше двух направлений. На пунктах, где имеется всего лишь два направления, измерения производят способом отдельного угла (способом приёмов) без замыкания горизонта. Количество приемов зависит от типа теодолита и класса геодезической сети (табл.6.3); допуски на результаты измерений приведены в табл.6.4.

Количество приёмов измерения горизонтальных углов Таблица 6.3

Приборы	П О Л И Г О Н О М Е Т Р И Я
4 класс	1 разряд	2 разряд
Теодолит Т2 Теодолит Т5	-

В первом приёме отсчёт на начальное направление принимают 0⁰00’; в i- том приёме , где n – число приёмов.

Направления на стенные знаки в полигонометрии 4 класса измеряют тремя круговыми приёмами после окончания измерения углов по ходу.

Допуски на характеристики точности измерений углов в полигонометрии Таблица 6.4

Основные характеристики точности угловых измерений	Д о п у с к и
Для теодолита Т2	Для теодолита Т5
Расхождение направлений в полуприёмах Расхождение направлений в приёмах Колебание значений 2С в приёме Колебание между повторными наблюдениями начального направления (незамыкание горизонта)	8,0”   8,0” 12,0”   8,0”	0,2’   0,2’ -   0,2’

Подготовка к измерению горизонтального угла теодолитом заключается в правильной установке теодолита и визирных целей относительно центров пунктов, фиксирующих угол на местности. При установке теодолита и визирных целей на штативы их центрирование нужно выполнять с помощью оптического центрира.

В полигонометрии 4-го класса и 1-го и 2-го разрядов для ослабления влияния ошибок центрировки и редукции применяют так называемую трехштативную систему, которая предусматривает расстановку трех или более штативов с подставками под теодолит и визирную марку сразу на нескольких пунктах подряд и центрирование штативов с помощью оптического центрира (рис.6.4).

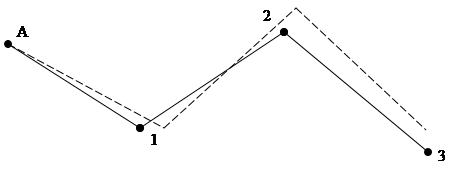Рис.6.4 – Трёхштативная система измерения углов и расстояний

На штативе пункта 1 устанавливают теодолит, а на штативах пунктов A и 2 - визирные марки. Для измерения следующего угла теодолит переносят на пункт 2, марку со штатива A - на штатив 1, а марку со штатива 2 - на штатив 3 и т.д. до конца хода. В результате измеренными оказываются углы так называемого "воздушного" полигонометрического хода, а не хода, образованного центрами пунктов. На угловую невязку хода влияют ошибки центрирования только на двух пунктах - на начальном и на конечном исходных пункттах хода.

Если для измерения сторон хода используется светодальномер или электронный тахеометр, то одновременно с измерением углов можно выполнить измерение сторон по тем же штативам.

Центрирование теодолита или штатива с подставкой с помощью оптического центрира можно выполнить по той же методике, что и с помощью нитяного отвеса, однако, на практике часто применяют так называемый "неправильный способ", который позволяет быстро и с нужной точностью выполнить сразу две операции: центрирование и горизонтирование подставки или теодолита. Порядок действий в этом способе:

1. штатив установить примерно над центром пункта;

2. вращая подъемные винты (любые и в произвольном направлении) совместить в поле зрения окуляра оптического центрира изображение центра пункта Ц с центром концентрических окружностей С;

3. вращая алидаду, установить уровень при алидаде горизонтального круга параллельно линии, соединяющей острия двух ножек штатива;

4. уменьшая или увеличивая длину одной из этих ножек, установить пузырек уровня в нульпункт с точностью одно-два деления,

5. повернуть алидаду на 90⁰ (т.е. установить уровень по третьей ножке штатива);

6. изменяя длину этой ножки, привести пузырек уровня в нульпункт с точностью одно-два деления.

Действия со 2-го по 6-е составляют одно приближение. Если центр пункта располагается в плоскости Т, проходящей через острия трех ножек штатива, то достаточно одного - двух приближений. Если центр пункта находится выше или ниже плоскости Т, то после 1-го приближения следует сначала оценить в поле зрения оптического центрира расстояние от центра пункта до точки C – центра концентрических окружностей. При выполнении 2-й операции 2-го приближения следует установить центр Ц на некотором расстоянии от центра C; величину и направление этого расстояния следует оценивать опытным путём.

В заключение точное горизонтирование теодолита (подставки) выполняют подъёмными винтами, то есть, приводят пузырёк уровня точно в нульпункт по обычной методике.

Способ круговых приёмов. На пункте стояния теодолита выбирают начальное направление с хорошей видимостью; остальные направления нумеруют по

Дата добавления: 2014-01-11