Крутое восхождение неэффективно

Принимать решения при неэффективном движении по градиенту гораздо сложнее. Принятие решений во многом зависит от определенности ситуации (далеко от оптимума, близко, неопределенно) и от адекватности линейной моде­ли. Наиболее типичные случаи показаны на блок-схеме.

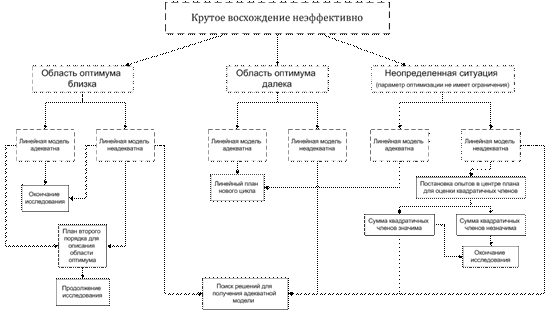
Рисунок 9

Рассмотрим каждую ситуацию отдельно.

Область оптимума близка. Если при реализации матрицы планирования удалось получить достаточно высо­кие значения параметра оптимизации и при крутом восхож­дении улучшить их не удалось, то наиболее типичными яв­ляются решения: 1) окончание исследования (выбирается лучший опыт); 2) построение плана второго порядка для описания облает оптимума.

Если линейная модель была неадекватна, то возможно третье решение – возврат к блок-схеме, чтобы выяснить причины неадекватности линейной модели.

Крутое восхождение неэффективно. Положение оптимума неопределенное. Если нет информации о положении оптимума и на стадии крутого восхождения не удалось
улучшить значение параметра оптимизации, то можно рекомендовать поставить опыты в центре эксперимента с тем, чтобы оценить вклад квадратичных членов. При значимой сумме можно приступать к достройке линейного плана до плана второго порядка, так как наличие квадратичных членов свидетельствует о близости к почти стационарной области.

Обратим внимание на то, что при незначимой сумме обратного вывода делать нельзя, ибо возможен, например, такой случай: b ₁₁ = 5,7, b ₂₂ = –5,З, b ₁₁ + b ₂₂ = +0,4. Сумма незначима, так как коэффициенты имеют разные знаки.

Это случай, когда имеется два оптимума. Если же есть основание полагать, что оптимум один, то при незначимой сумме квадратичных членов можно приступить ко второму циклу крутого восхождения.

Дата добавления: 2014-01-11