Функции нескольких переменных. Частные приращения и частные производные

Частные приращения и частные производные

Для функции 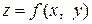частными приращениями по х и по y называется соответственно

,

.

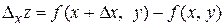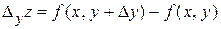Частной производной функции нескольких переменных по некоторой переменной называется предел отношения частного приращения функции по этой переменной к приращению переменной, стремящемуся к нулю, т. е.

,

.

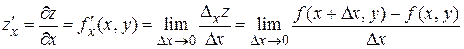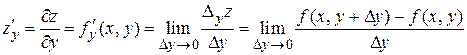Для функции 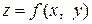не имеют смысла запис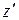и или .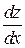

Не существует просто производная функции 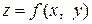, а существуют только частные производные по х и по y, обозначаемые 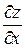и .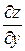

Можно сформулировать следующее правило нахождения частных производных функций нескольких переменных. Для того чтобы найти частную производную функции нескольких переменных по некоторой переменной, необходимо все независимые переменные функции кроме данной считать постоянными и найти производную как от функции одной переменной.

Пример 3.5. Найти частные производные функции .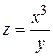

Когда ищем производную по х, считаем y постоянной, т. е. можно вынести множитель 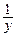за знак дифференцирования. .

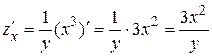Когда находим частную производную по y, то считаем 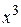постоянной.

.

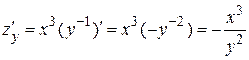Пример 3.6. Найти частные производные функции .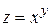

При нахождении производной по х переменной является х, а y является постоянной, поэтому производная ищется как от степенной функции (по формуле 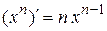). Находим .

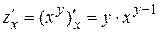Когда находим производную по y, то постоянной является х и производная ищется как от показательной функции (по формуле ).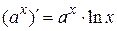

Находим .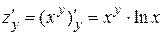

Пример 3.7. Найти частные производные функции .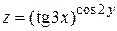

Здесь в основании стоит не просто х, а tg3 x, поэтому необходимо находить частную производную по х как от сложной функции

.

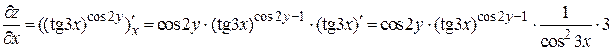Так же частная производная по y находится как производная сложной функции

.

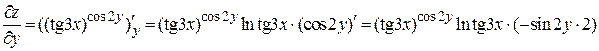Пример 3.8. Найти эластичность функции Кобба-Дугласа 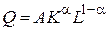по независимым переменным K и L.

Используем определение эластичности функции 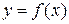одной переменной 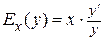. Находим .

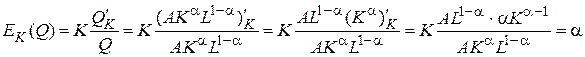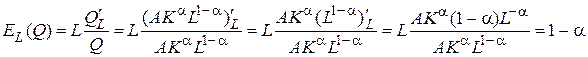
Дата добавления: 2014-01-11