Градиент функции, его свойства

Градиентом функции 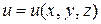называется вектор

,

где 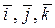- единичные векторы координатного базиса в прямоугольной декартовой системе координат.

Кратко можно записать 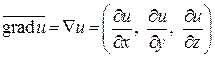. Здесь Ñ - знак набла.

Пример 3.22. Найти градиент функции 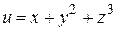в точке .

.

.

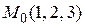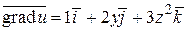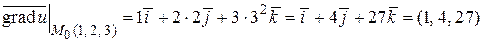Теорема 3.5. Производная функции 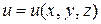по направлению вектора 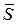равняется проекции градиента этой функции на это направление, т. е.

.

Известно, что проекция некоторого вектора 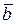на направление вектора 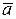равняется

.

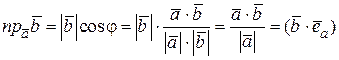Здесь j - угол между векторам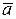и и 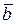, 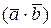- скалярное произведение векторов, 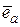- единичный вектор, совпадающий по направлению с вектором .

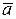Найдем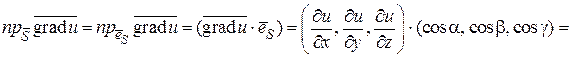

.

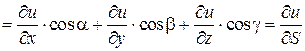Свойство 1. Производная функции 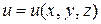по направлению вектора 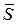достигает своего наибольшего значения, если направление вектора 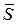совпадает с направлением градиента этой функции.

Действительно, производную данной функции по направлению вектора 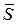можно записать следующим образом 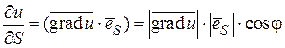, где j - угол между градиентом и вектором 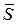. Если этот угол равен нулю j = 0, то косинус этого угла и производная функции принимают наибольшие значения, cos0 = 1, .

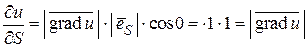Свойство 2. Производная функции 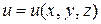по направлению вектора 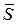равняется нулю, если направление вектора 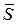перпендикулярно направлению градиента этой функции.

Действительно, .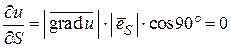

Данные свойства используются при решении задач оптимизации (нахождения наибольшего, наименьшего значений функций) с помощью численных методов. Градиент функции определяет направление наибольшего изменения функции. Направление перпендикулярное градиенту определяет направление, в котором функция не изменяется.

Известно, что на поверхности уровня 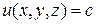функция 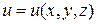не изменяется. Следовательно, градиент функции перпендикулярен поверхности уровня. Это обстоятельство можно использовать для написания уравнения касательной плоскости к поверхности 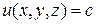. Пусть точка 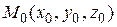принадлежит поверхности. Найдем градиент функции 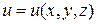в этой точке 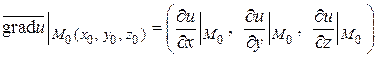и напишем уравнение плоскости, проходящей через точку 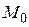перпендикулярно вектору 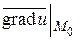. Получаем уравнение касательной плоскости

.

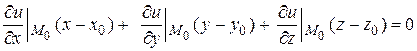Пример 3.23. Написать уравнение касательной плоскости к эллипсоиду

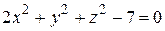в точке .

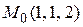Находим ,, ; , , .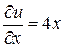

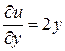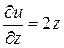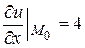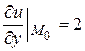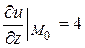Записываем уравнение касательной плоскости

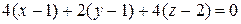Û .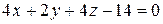

Дата добавления: 2014-01-11