Определение: Составные высказывания, истинные при любых значениях истинности входящих в них элементарных высказываний, принято называть тавтологиями

Эквиваленция высказываний А и В – это конъюнкция прямой и обратной импликаций высказываний А и В.

Высказываний

А	В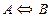
и и л л	и л и л	и л л и

Другое определение эквиваленции двух высказываний:

	(5)

Определение:

Докажем утверждение (5): .

Задание: 1) покажите, что высказывания, данные на стр. 68 (учебника) являются тавтологиями.

2) привести примеры других тавтологий.

Законы операций над высказываниями.

1) 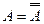закон двойного отрицания (доказан ранее);

2) 2.1 коммутативность конъюнкции,

2.2 дизъюнкции;

3) 3.1 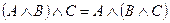ассоциативность конъюнкции и

3.2 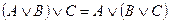дизъюнкции;

4.1 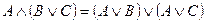закон дистрибутивности конъюнкции

относительно дизъюнкции;

4.2 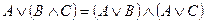дизъюнкции относительно конъюнкции;

5.1 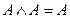законы идемпотентности;

5.2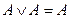

6) (абсолютно истинно) закон исключённого третьего

7) (абсолютно ложно) законпротиворечия

8.1 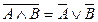законы де Моргана;

8.2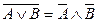

9) законы поглощения;

10) законы исключения импликации;

11)

12) закон исключения эквиваленции.

Все законы можно доказать с помощью таблицы истинности.

Второй способ доказательства путём преобразования выражений с помощью уже известных формул.

Докажем 8.2.: 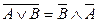с помощью таблицы истинности.

А	В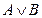
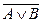
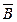
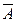
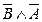
и и л л	и л и л	и и и л	л л л и	л и л и	л л и и	л л л и

Сделаем некоторые замечания:

1. Если высказывание составное, то его структура выражается конечной последованию букв А_1, А₂, А₃, … А_к, обозначающих элементарные высказывания, знаков операций, выполненных над элементарными высказываниями и скобок, определяющих порядок операций.

2. Условились считать, что сильнее всех связывает знак отрицания, за ним конъюнкция, дизъюнкция и импликация. Слабее всех связывает знак эквиваленции. Название высказывания определяется по последней операции. Например, 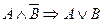– это импликация.

3. Конечная последовательность букв, знаков логических операций и скобок, выражающая логическую структуру высказывания, называется формулой логики высказывания.

4. Для выявления логической структуры высказывания надо:

а) выделить в нём все элементарные высказывания и обозначить их буквами;

б) логические связки заменить соответствующими им символами;

в) записать с помощью букв, знаков операций и скобок логическую структуру исходного высказывания.

Высказывательные формы (предикаты).

Дата добавления: 2014-01-11