
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обращение предиката в высказывание
|
|
|
|
Определение: Предложение с одной или несколькими переменными, которое обращается в высказывание при подстановке вместо переменных их значений, называется высказывательной формой или предикатом.
В зависимости от числа переменных предикаты бывают одноместными, двухместными и т.д. n –местные.
Обозначаются: А(х) – одноместный
В(х,y) – двухместный и т.д.
…
D(x1, x2, x3, … хn)
С каждым предикатом связывают три множества:
1) область определения предиката: DA(x) – это множество значений переменной, при которых предикат обращается в высказывание.
2) множество истинности предиката ТА(х) – это множество тех значений переменных из области определения предиката, при котором предикат обращается в истинное высказывание.
3) множество ложности предиката: 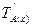 - это множество тех значений переменной, при котором предикат обращается в ложное высказывание.
- это множество тех значений переменной, при котором предикат обращается в ложное высказывание.
Между этими множествами существует вполне определённая связь:
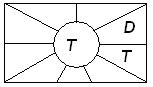 |

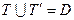

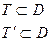
Множества истинности и множества ложности предиката дополняют друг друга до области определения предиката.
Пример 1. На множестве R задано предложение Х2 – 1 = 0. Является ли оно предикатом? Какова область определения? Множество истинности?
1)  Х2 – 1 = 0 – это предложение с переменной.
Х2 – 1 = 0 – это предложение с переменной.
2) при Х = 1, 12 – 1 = 0 – это предложение обращается в 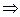
высказывание.
это одноместный предикат: А(х): Х2 – 1 = 0
DA =R.
ТА = 

Видим, что все отношения выполняются: 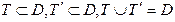 .
.
Пример 2: Дано предложение: при x = -1 выполняется равенство x + 1 = 0.
1) – это предложение с переменной, но оно является истинным высказыванием, а не предикатом.
Пример 3: С(х,у): x + y = 7, 
1) предложение с двумя переменными х и y
2) обращается в высказывание, например, при x = 3 y = 5
С (3,5): 3 + 5 = 7 – высказывание (не важно сейчас какое).
Dc – это множество пар действительных чисел:
Dс = 

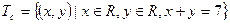 , т.е. множество таких пар действительных чисел, для которых верно: x + y = 7.
, т.е. множество таких пар действительных чисел, для которых верно: x + y = 7.


Если подставлять значение только одной переменной, то предикат станет одноместным предикатом.
Пусть x = 10 тогда  - это одноместный предикат.
- это одноместный предикат.
Предикат можно обратить в высказывание двумя способами:
1 способ: путём подстановки в предикат конкретного значения переменной (переменных)
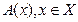 и пусть
и пусть  , где
, где  тогда
тогда  - высказывание.
- высказывание.
2 способ: путём навешивания кванторов.
Кванторы бывают двух видов:
1) квантор всеобщности, который выражается словами: любой, каждый, всякий, все, и обозначается: 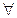 .
.
2) квантор существования: выражается словами: найдётся, существует, и обозначается  .
.
Пусть на множестве Х задан одноместный предикат А(х). Предложение: для любого Х из множества Х выполняется А(х) – это высказывание, которое ложно, если найдется хотя бы одно значение переменной x  Х, при котором А(х) обращается в ложное высказывание. Если таких значений переменной нет, то это предложение – истинное высказывание. Запишем это высказывание так:
Х, при котором А(х) обращается в ложное высказывание. Если таких значений переменной нет, то это предложение – истинное высказывание. Запишем это высказывание так: 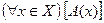 .
.
Предложение: существуют элементы x  Х такие, что выполняется А(х) – высказывание, которое истинно, если существует хотя одно бы одно значение переменной из множества Х, при котором А(х) – истинное высказывание. Если таких значений нет, то это предложение ложное высказывание.
Х такие, что выполняется А(х) – высказывание, которое истинно, если существует хотя одно бы одно значение переменной из множества Х, при котором А(х) – истинное высказывание. Если таких значений нет, то это предложение ложное высказывание.
Запишем это высказывание так:  .
.
Пусть  - одноместный предикат. Навесим на него кванторы:
- одноместный предикат. Навесим на него кванторы:
1) 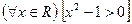 - высказывание. Определим его значение истинности.
- высказывание. Определим его значение истинности.
Пусть x = 0. А(0): 02- 1>0 – ложь 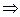
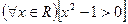 - ложное высказывание.
- ложное высказывание.
2)  - высказывание. Определим его значение истинности.
- высказывание. Определим его значение истинности.
Пусть х = 2  . Тогда А (2): 22 - 1 > 0 – «И»
. Тогда А (2): 22 - 1 > 0 – «И» 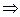
 - истинное высказывание.
- истинное высказывание.

|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 2465; Нарушение авторских прав?; Мы поможем в написании вашей работы!