Для того, чтобы натуральное число необходимо и достаточно, чтобы десятичная запись этого числа оканчивалась цифрой 0

Выпишем, как читаются основные высказывания, связанные с отношениями логического следования и равносильности на русском и логическом языке:

На русском языке	На логическом языке
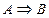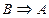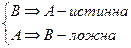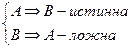1) Адостаточное условие для В. 2) Анеобходимое условие для В.     3) Анеобходимое, но не достаточное условие для В.     4) Адостаточное, но не необходимое условие для В.     5) Анеобходимое и достаточное условие для В.	1) - истинна. 2) - истинна.   3)   4)   5)

Замечание: Необходимые и достаточные условия в математике называются признаками.

Строение теоремы. Виды теорем

Теоремой, как правило, называют истинное доказуемое утверждение. Иногда теоремой называют утверждения, которые ложны, или которые ещё не доказаны.

Абсолютное число теорем можно сформулировать в форме импликации.

Например: если четырёхугольник ромб, то его диагонали взаимно перпендикулярны.

А так как всякая теорема утверждается на всей области определения, то кратко пишут

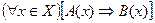(I)

В теоремах различают 3 части: разъяснительная часть (преамбула). В ней даются пояснения к обозначениям, описываются множества к элементам которых относится теорема, т.е. указывается область определения предикатов А(х) и В(х).

Условие теоремы: предикат А(х).

Заключение теоремы: предикат В(х).

Слова если … то ни к А(х), ни к В(х) не относятся.

Назовём теорему (I) прямой.

1. 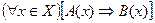прямая теорема;

2. 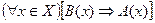- обратнаяк прямой:

3. 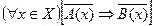- противоположная к I (прямой)

4. - противоположная к II (обратной)

Выделим названные части в теореме: если четырехугольник ромб, то его диагонали взаимно перпендикулярны.

«На множестве четырёхугольников» – преамбула (как правило, не произносится);

«Четырехугольник x – ромб» - условие теоремы;

«Диагонали четырехугольника x- взаимно перпендикулярны» - заключение теоремы.

Сформулируем теоремы 1-4.

1. Если четырехугольник x – ромб, то его диагонали взаимно перпендикулярны. – истинное утверждение.

2. Если диагонали четырёхугольника x взаимно перпендикулярны, то четырёхугольник x – ромб.– утверждение ложное, т.к. существует четырехугольник, у которого диагонали взаимно перпендикулярны, не

являющийся ромбом.

3. Если четырёхугольник Х – не ромб, то его диагонали не взаимно перпендикулярны. – ложное утверждение.

4. Если диагонали четырёхугольника не взаимно перпендикулярны, то четырёхугольник не является ромбом. – истинное утверждение.

Дата добавления: 2014-01-11