Аналитические методы статического анализа

Задача анализа цепи по постоянному току состоит в получении зависимостей, связывающих токи и напряжения на полюсах активных электронных компонентов с параметрами пассивных компонентов и задающими величинами источников питания. Полученные зависимости используют для расчета параметров пассивных компонентов, обеспечивающих требуемые режимы работы активных электронных компонентов.

Анализ электронной схемы включает в себя формирование схемной модели (схемы замещения) и математической модели исходной схемы. Схемная модель формируется на основании метода, выбранного для описания математической модели заданной схемы (метод узловых потенциалов, метод контурных токов и т.п.). Нами для формирования математической модели выбран метод узловых потенциалов. В дальнейшем необходимо об этом помнить, поскольку все преобразования при формировании схемной модели проводятся для случая применения именно этого метода.

Схему замещения электронной цепи по постоянному току получают из схемы электрической принципиальной, используя следующие правила:

– ветви с емкостными элементами размыкают;

– идеальные индуктивности закорачивают;

– ветви идеальных источников переменного тока размыкают;

– идеальные источники переменных э.д.с. закорачивают;

– активные электронные компоненты представляют соответствующими условными графическими обозначениями либо замещают эквивалентными схемами для постоянного тока;

– источники питания постоянного тока принято представлять источниками постоянных э.д.с. или постоянных токов с внутренними сопротивлениями.

В качестве примера рассмотрим формирование схемы замещения по постоянному току двухкаскадного усилителя низкой частоты на биполярных транзисторах с общей отрицательной обратной связью по постоянному току (рис. 3.17).

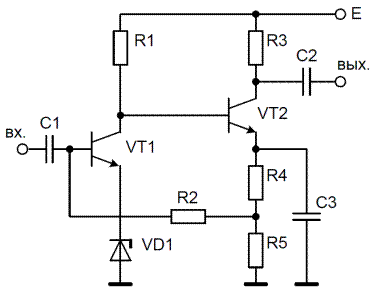
Рис. 3.17. Схема двухкаскадного усилителя низкой частоты на биполярных транзисторах с общей отрицательной обратной связью по постоянному току

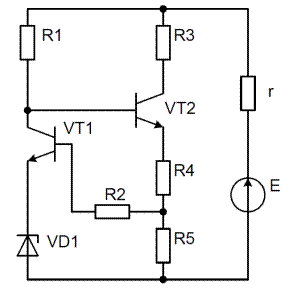
Рис. 3.18. Схема замещения двухкаскадного усилителя низкой частоты по постоянному току

В соответствии с правилами построения схем замещения по постоянному току в схеме (рис. 3.17) размыкаем ветви, содержащие конденсаторы C1, C2, C3. Источник питания Е представляем идеальным источником э.д.с. Е с последовательно включенным внутренним сопротивлением r (часто при составлении схемы замещения принимают r = 0). Активные электронные компоненты (транзисторы VT1, VT2 и стабилитрон VD1) представляем соответствующими условными графическими обозначениями и устраняем пересечение ветвей, содержащих резистор R2 и стабилитрон VD1. Полученная схема замещения усилителя по постоянному току представлена на рис. 3.18.

Для формирования математической модели в полученной схеме замещения (рис. 3.18) следует заменить их эквивалентными схемами для постоянного тока, например нелинейными моделями.

Рассмотрим процесс формирования математической модели схемы.

Пусть после указанных выше преобразований схема приобрела вид, показанный на рис. 3.19. Найдем потенциалы всех узлов и токи всех ветвей. Исходные данные: J = 1 А, Е = 1 В, R ₁ = 1 Ом, R ₂ = 2 Ом, R ₃ = 4 Ом, R ₄ = 5 Ом, R ₅ = 8 Ом, R ₆ = 10 Ом.

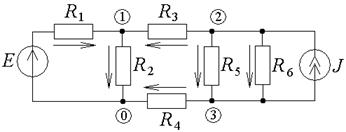
Рис. 3.19. Схема для проведения статического анализа

Обозначим узлы схемы номерами от 0 до 3 (узлы, находящиеся справа от узлов 2 и 3, мы никак не обозначили, поскольку они имеют такие же потенциалы). Приравняем потенциал одного из узлов схемы (узла 0) к нулю, а для всех оставшихся узлов составим систему уравнений по методу узловых потенциалов:

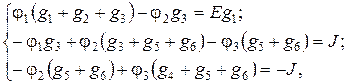(3.1)

где g ₁, g ₂, g ₃, g ₄, g ₅, g ₆ – проводимости ветвей с сопротивлениями R ₁, R ₂, R ₃, R ₄, R ₅, R ₆ соответственно (g = 1/ R).

Решаем данную систему уравнений любым из известных способов. Если число неизвестных больше двух, как в данном случае, систему удобнее решать не методом подстановки, а матричным методом (методом Крамера). В матричном виде система уравнений (3.1) будет выглядеть

Найдем сначала определитель матрицы проводимостей:

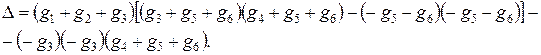
С учетом приведенных значений сопротивлений и параметров источников J и E имеем D» 0,238 См³.

Для определения потенциалов узлов j₁, j₂ и j₃ необходимо предварительно найти определители матриц, полученных из матрицы проводимостей путем подстановки столбца с источниками токов вместо первого, второго и третьего столбцов матрицы соответственно:

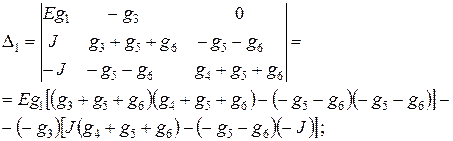
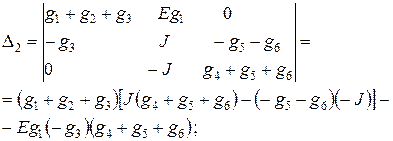
Подставив известные значения проводимостей, E и J, получим D₁» 0,2 В×См³, D₂» 0,46 В×См³, D₃» – 0,32 В×См³. Теперь можно найти потенциалы узлов схемы:

Зная потенциалы узлов схемы, можно определить также и токи ветвей. Обозначим токи, протекающие через резисторы R ₁, R ₂, R ₃, R ₄, R ₅, R ₆, соответственно I_{R 1}, I_{R 2}, I_{R 3}, I_{R 4}, I_{R 5}, I_{R 6}. Тогда, с учетом показанных на рис. 11 направлений токов, их значения можно определить как

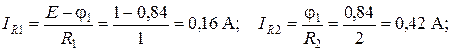
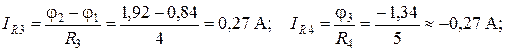
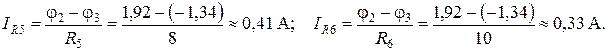
Полученное отрицательное значение тока I_{R 4} означает, что его истинное направление противоположно показанному на рис. 3.19.

Проверим правильность решения с помощью Первого закона Кирхгофа: для любого узла схемы сумма всех втекающих в него токов должна быть равна сумме вытекающих. Так, например, для узла 2 должно выполняться равенство I_{R 1} + I_{R 3} = I_{R 2}. Действительно, 0,16 + 0,27 = 0,43 ≈ ≈ 0,42 А. Небольшая погрешность, связанная с округлениями промежуточных и конечных результатов, вполне допустима.

Аналогично можно удостовериться в выполнимости Первого закона Кирхгофа и для остальных узлов схемы.

Дата добавления: 2014-01-11