
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение натуральной величины отрезка прямой общего положения методом прямоугольного треугольника
|
|
|
|
Ортогональная проекция отрезка прямой общего положения на любую плоскость проекций всегда меньше длины самого отрезка. Для определения натуральной величины отрезка прямой служит метод прямоугольного треугольника, который заключается в следующем.
Предположим, что точки А и В лежат в I октанте (рис. 20, а). Соединим эти точки и получим отрезок некоторой прямой АВ.
 |
Из точки А проведем линию параллельную А ¢ В ¢, которая в пересечении с линией проекционной связи даст точку В 0.
Рассмотрим прямоугольный треугольник АВВ О:
- гипотенуза АВ определяет истинную величину этого отрезка;
- катет АВ 0 равен горизонтальной проекцией А ¢ В ¢;
- катет ВВ 0 равен D z = zВ – zА.
На ортогональном чертеже оказывается достаточно данных для построения на чертеже треугольника, равного рассмотренному (рис. 20, б). Для этого к горизонтальной проекции А ¢ В ¢ «пристроен» второй катет - разность координат D z. Гипотенуза построенного треугольника есть натуральная величина отрезка АВ.
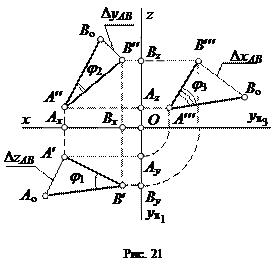 Если прямоугольный треугольник строится на фронтальной проекции, то второй катет окажется равным разности координат D y (табл. 3). Для треугольника, построенного на профильной проекции, вторым катетом будет D x (рис. 21).
Если прямоугольный треугольник строится на фронтальной проекции, то второй катет окажется равным разности координат D y (табл. 3). Для треугольника, построенного на профильной проекции, вторым катетом будет D x (рис. 21).
Координаты концов отрезка могут иметь разные знаки. Тогда разность координат определяется с учетом знака. Например, если координата z точки А положительная, а точки В отрицательная, то разность координат будет равна
D zАВ = z A – (- z B) = z A + z B.
Таблица 3
Геометрические элементы при определении истинной величины отрезка прямой методом прямоугольного треугольника
| Проекция отрезка прямой, выбираемая в качестве первого катета треугольника | Разность координат, откладываемая в качестве второго катета | Плоскость проекций, к которой определяется угол наклона | Обозначение угла наклона |
| горизонтальная: А ¢ В ¢ | D zАВ =| A z B z| | p1 | j1 |
| фронтальная: А ² В ² | D yAB =| A y B y| | p2 | j2 |
| профильная: А ¢¢¢ В ¢¢¢ | D xAB =| A x B x| | p3 | j3 |
В общем случае натуральная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого является проекция отрезка прямой, а вторым - разность «третьих» координат.
Угол наклона прямой к плоскости проекций – это угол между прямой и ее проекцией. Следовательно, определяя истинную величину отрезка прямой методом прямоугольного треугольника, одновременно можно найти и угол ее наклона к плоскости проекций (j 1, j 2, j 3). Угол между гипотенузой и соответствующей проекцией отрезка равен углу наклона этой прямой к данной плоскости проекций.

Пример 3. Определить истинную величину отрезка АВ и угол наклона к плоскости p1 (рис. 22).
1. По таблице 3 определяем, что для нахождения угла наклона к плоскости p1 надо построить прямоугольный треугольник, в котором одним катетом будет горизонтальная проекция отрезка А ¢ В ¢, а вторым – разность координат по оси z.
2. Определяем координаты по оси z точек А и В и их разность:
D zАВ = zВ – (- zА) = zВ + zА .
3. Строим прямоугольный треугольник, в котором за катет принимаем горизонтальную проекцию А ¢ В ¢. В качестве второго катета откладываем расстояние, равное D zАВ.
4. Гипотенуза построенного треугольника есть истинная величина отрезка АВ, а угол при вершине А ¢ (угол j 1) – угол наклона прямой к плоскости p1.
Лекция 3
СЛЕДЫ ПРЯМОЙ
Следом прямой называется точка пересечения прямой линии с плоскостью проекций (является точкой частного положения – лежит в плоскости проекций).
Прямая общего положения пересекает все три плоскости проекций и, следовательно, имеет три следа. Прямая линия частного положения не имеет следа на плоскости проекций, если она параллельна этой плоскости.
Выберем две точки: точку М, лежащую в плоскости проекций p1, и точку N – в плоскости проекций p2 (рис. 23, а). Через эти точки проведем прямую.
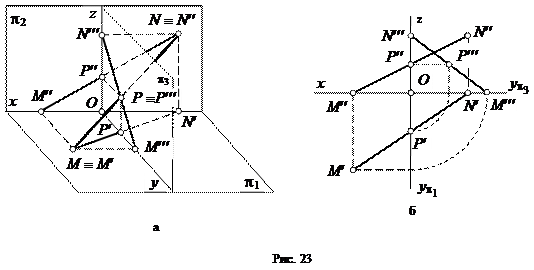 |
Точка пересечения (M) прямой линии с горизонтальной плоскостью проекций называется горизонтальным следом прямой; точка пересечения (N) прямой линии с фронтальной плоскостью проекций называется фронтальным следом прямой; точка пересечения (P) прямой линии с профильной плоскостью проекций называется профильным следом прямой.
Следы прямой совпадут с проекциями этих следов в той плоскости, где они расположены: М º M ¢, N º N ¢¢, P º P ¢¢¢.
Поскольку точка М лежит в плоскости p1, то ее фронтальная проекция М ¢¢ располагается на оси x, а профильная М ¢¢¢ – на оси y. Горизонтальная проекция точки N - N ¢ также располагается на оси x, а профильная проекция N ¢¢¢ лежит на оси z. Горизонтальная проекция профильного следа P ¢ лежит на оси y, а фронтальная проекция P ¢¢ - на оси z.
Охарактеризуем положение каждой проекции каждого из трех следов на ортогональном чертеже (рис. 23, б).
1) Построение проекций горизонтального следа:
M ¢¢ - фронтальная проекция горизонтального следа лежит на пересечении фронтальной проекции прямой с осью x;
М ¢ - горизонтальная проекция горизонтального следа лежит на пересечении линии проекционной связи, проведенной из проекции M ¢¢ перпендикулярно оси x, с горизонтальной проекцией прямой;
M ¢¢¢ - профильная проекция горизонтального следа лежит на пересечении профильной проекции прямой с осью y p3.
2) Построение проекций фронтального следа:
N ¢ - горизонтальная проекция фронтального следа лежит в точке пересечения горизонтальной проекции прямой с осью x;
N ¢¢ - фронтальная проекция фронтального следа лежит на пересечении фронтальной проекции прямой с линией проекционной связи, проведенной из точки N ¢ перпендикулярно оси x;
N ¢¢¢ - профильная проекция фронтального следа лежит на пересечении профильного следа прямой с осью z.
3) Построение проекций профильного следа:
P ¢ - горизонтальная проекция профильного следа лежит на пересечении горизонтальной проекции прямой с осью y p1.
P ¢¢ - фронтальная проекция профильного следа лежит на пересечении фронтальной проекции прямой с осью z.
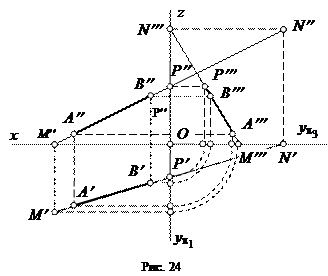
|

6. По двум проекциям фронтального следа N ¢ и N ¢¢ строим третью его проекцию - N ¢¢¢, которая совпадает с точкой пересечения профильной проекции прямой с осью z.
7. В пересечении А ¢ В ¢ с осью y p1строим точку Р ¢ (горизонтальную проекцию профильного следа).
8. В пересечении А ² В ² с осью z получаем точку фронтальную проекцию профильного следа - Р ².
9. По двум проекциям Р¢ и Р¢¢ строим профильную проекцию - Р¢¢¢ (проекции Р¢¢ и Р¢¢¢ находятся на горизонтальной линии проекционной связи).
ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
Две прямые могут пересекаться, быть параллельными друг другу и скрещиваться.
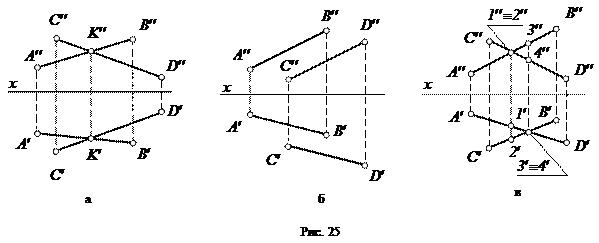
1) Пересекающиеся прямые имеют одну общую точку. Если прямые линии пересекаются, то одноименные проекции этих прямых тоже пересекаются (рис. 25, а), причем проекции точки пересечения лежат на одной линии проекционной связи.
2) Параллельные прямые лежат в одной плоскости и не имеют общих точек. Одноименные проекции двух параллельных прямых параллельны между собой (рис. 25, б).
3) Скрещивающиеся прямые, в отличие от пересекающихся и параллельных прямых, не лежат в одной плоскости. Хотя одноименные проекции двух скрещивающихся прямых и могут пересекаться, но точки их пересечения не могут лежать на одной линии проекционной связи (рис. 25, в).
Две точки, лежащие на скрещивающихся прямых и на одном перпендикуляре к плоскости проекций, называются конкурирующими. Проекции конкурирующих точек лежат в точке пересечения одноименных проекций скрещивающихся прямых (точки 1 и 2 на фронтальной плоскости проекций, точки 3 и 4 на горизонтальной плоскости проекций – см. рис. 25, в).
Построение их проекций применяется для определения взаимной видимости геометрических элементов1.
 |

(которые совпадают с самими следами), которые обозначаются соответственно h ¢0a, f ²0a и p ¢¢¢0a. Каждый след плоскости проходит через две точки схода следов. Следовательно, любые два следа плоскости позволяют определить все три параметра плоскости.
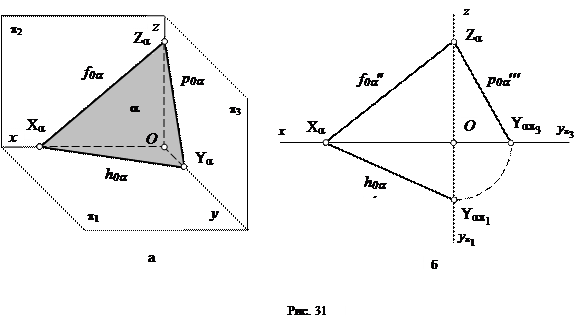
Таким образом, любые два следа плоскости однозначно определяют ее положение в пространстве. Также как положение точки в пространстве определяются тремя ее координатами, так и положение плоскости может быть задано аналитически тремя ее параметрами.
Плоскость, пересекающая все три плоскости проекций, называется плоскостью общего положения. Если плоскость параллельна одной или двум осям координат, то она называется плоскостью частного положения.
ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ
Плоскости, параллельные одной оси координат
1) Плоскость, параллельная оси z (рис. 32).
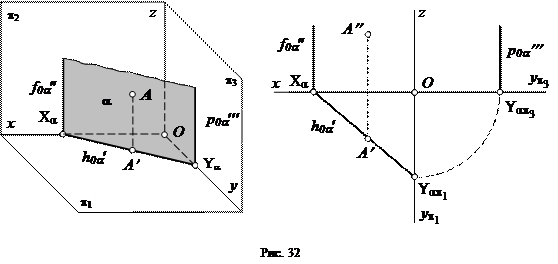 |
У такой плоскости параметры Хa, и Ua - конечные величины, а параметр Za = ¥. Следовательно, фронтальный и профильный следы такой плоскости, которые должны пройти через точку схода следов Za, будут параллельны оси z. Плоскость, параллельная оси z перпендикулярна горизонтальной плоскости проекций и называется горизонтально-проецирующей плоскостью.
Рассмотрим точку А, лежащую в горизонтально-проецирующей плоскости a, и построим горизонтальную проекцию этой точки. Для этого из точки А опустим перпендикуляр на плоскость проекций p1. Горизонтальная проекция любой точки, лежащей в горизонтально-проецирующей плоскости, будет всегда располагаться на горизонтальном следе плоскости.
4) Плоскость, параллельная оси y (рис. 33).
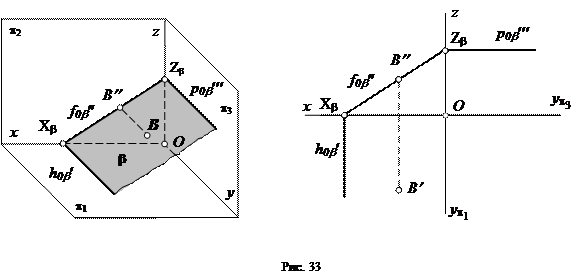 |
Если плоскость параллельна оси y, то ее параметр по этой оси равен бесконечности (Yb = ¥) и, следовательно, горизонтальный и профильный следы плоскости будут параллельны оси y. Плоскость, параллельная оси y, перпендикулярна фронтальной плоскости проекций p2 и называется фронтально-проецирующей плоскостью.
Фронтальная проекция любой точки, лежащей в этой плоскости (например, точки В), всегда расположена на фронтальном следе плоскости.
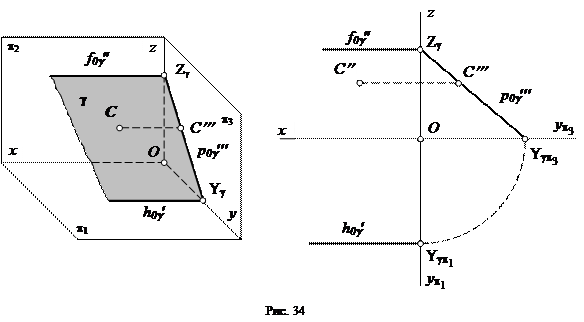
4) Плоскость, параллельная оси x (рис. 34).
У такой плоскости параметр по оси x равен бесконечности (Хg = ¥), поэтому ее фронтальный и горизонтальный следы будут параллельны оси x. Такая плоскость перпендикулярна профильной плоскости проекций p3 и называется профильно-проецирующей плоскостью.
Профильная проекция любой точки, лежащей в этой плоскости (например, точки С), всегда расположена на профильном следе плоскости.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 633; Нарушение авторских прав?; Мы поможем в написании вашей работы!