Введение. Для того, чтобы первый закон термодинамики выразить в дифференциальной форме необходимо было ввести понятие о физических величинах как функциях состояния и

Для того, чтобы первый закон термодинамики выразить в дифференциальной форме необходимо было ввести понятие о физических величинах как функциях состояния и величинах, которые являются функциями процесса. Подобная ситуация имеет место и для второго закона термодинамики. В этом случае его математическое выражение зависит от типа процесса. С позиций второго закона термодинамики все процессы разделяются на два класса, которые принято называть термодинамически обратимыми и термодинамически необратимыми. Термодинамически необратимые процессы – это процессы, которые проходят обычным, естественным образом под действием тех или иных движущих сил. Например, подвод тепла к какому-то веществу вызывает процесс изменения внутренней энергии, который обнаруживается по повышению температуры. Замечательным примером термодинамически необратимого процесса являются химические реакции, когда после смешения некоторых веществ наблюдается самопроизвольный процесс образования продуктов.^*

Термодинамически обратимый процесс более сложное понятие и мы пока ограничимся его констатацией.

Для термодинамически обратимого процесса второй закон термодинамики выражается уравнением (1)

а для термодинамически необратимого процесса соотношением (2)

_____________________

^* Ниже будут рассмотрены движущие силы, под действием которых проходят самопроизвольные реакции.

Здесь δQ элементарная теплота, которой обменивается система с окружающей средой в обратимом и необратимом процессах при температуре Т. Отношение δQ/Т называется приведенной теплотой. Символ S обозначает физическую величину, которую немецкий физик Клаузиус (1822 – 1888) назвал энтропией. Существование энтропии было установлено не экспериментально, а подобно внутренней энергии, в результате доказательства определенного математического уравнения, в данном случае описывающего термодинамически обратимый процесс. Клаузиус, основываясь на работе французского физика Сади Карно (1796 – 1832), доказал^*, что

(3)

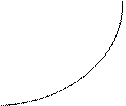
где обозначает интегрирование по контуру L, который описывает циклический термодинамически обратимый процесс. Таким циклом в координатах Р – V может быть условный цикл, представленный на рис.1.

Р

Рис. 1 Контур произвольного термодинамически обратимого цикла

В процессе перехода системы из состояния 1 в состояние 2, а затем в направлении 2 → 1 происходит обмен теплотой при непрерывно меняющейся температуре Т, которая в соответствии с уравнением (1) является параметром процесса. Контур процесса, заданный в математическом виде, и является кривой _____________________

^* Доказательство уравнения (3) приводится во многих пособиях по физической химии, например, «Курс физической химии» под редакцией Я.Н. Герасимова, изд. Химия. Москва, 1969.

интегрирования (L) интеграла (3).

Из уравнения (3) непосредственно следует уравнение (1). В основе такого заключения лежит теорема: если криволинейный интеграл по замкнутому контуру равен нулю, подинтегральное выражение есть полный дифференциал некоторой функции, в данном случае S.

После интегрирования соотношений (1) и (2) имеем

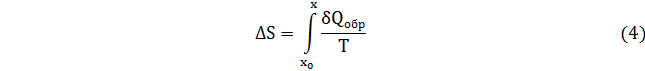
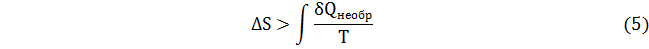
(К)

Для вычисления интеграла (4) необходимо задать δQ в виде выражения, зависящего от Т или δQ и Т представить в виде другого выражения, зависящего, например, от параметра х.

В литературе вместо выражения термодинамически обратимый и термодинамически необратимый обычно используется сокращенная терминология – обратимый и необратимый процессы.

За редким исключением величина интеграла по необратимому пути К неизвестна, но соотношения в виде неравенств (2) и (5) доказаны строго.

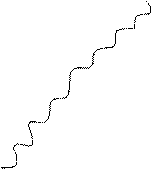
Рассмотрим произвольный процесс, в котором система переходит из состояния 1 в состояние 2 термодинамически обратимо (путь а) и любым произвольным способом термодинамически необратимо (путь б), рис. 2.

2

а

б

1

Рис.2. Пути перехода системы из состояния 1 в состояние 2

Исходя из соотношения (4), (5) и учитывая, что энтропия функция состояния, изменение энтропии в этих процессах можно выразить следующим образом

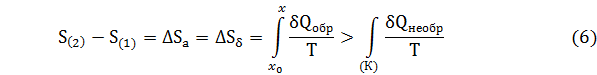
где S₍₂₎, S₍₁₎ – значение энтропии системы в конечном и начальном состояниях, К – условный путь необратимого процесса, который математически точно в сущности описать невозможно.

Из выражения (6) следует, что хотя изменение энтропии не зависит от пути процесса, вычислить это выражение можно лишь по уравнению (), описывающему обратимый процесс.

В самом общем виде термодинамически обратимый процесс можно определить как процесс, в котором при проведении его в прямом направлении, а потом в обратном, в исходное состояние возвращается не только система, но и окружающая среда, при взаимодействии с которой совершается процесс. Другими словами изменения, которым подвергается система и окружающая среда при проведении процесса в прямом направлении полностью компенсируются изменением системы и окружающей среды, когда процесс проводится в обратном направлении. Это, пока общее и абстрактное условие не выполняется для всех реальных, естественных процессов. В этом смысле они термодинамически необратимы.

Если хотя бы одна из стадий циклического процесса термодинамически необратима, процесс в целом необратим.

В циклическом необратимом процессе в исходное состояние возвращается только система. В отличие от этого окружающая среда при завершении процесса находится в состоянии, которое отличается от состояния в начале процесса.

Дата добавления: 2014-01-11