Средняя квадратическая погрешность арифметического среднего

Арифметическое среднее определяется выражением:

,

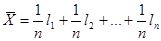где 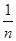- некоторое постоянное число. Если среднюю квадратическую погрешность арифметического среднего обозначить через М, а среднюю квадратическую погрешность одного измерения через m, то согласно можно записать:

М² = 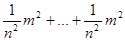, откуда М = ,

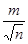Т.е. средняя квадратическая погрешность арифметического среднего в раз меньше средней квадратической погрешности одного измерения.

Это свойство средней квадратической погрешности арифметического среднего позволяет повысить точность измерений путем увеличения числа измерений. Например, требуется определить величину угла с точностью 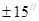при наличии 30-секундного теодолита. Очевидно, что если измерить угол 4 раза и определить арифметическое среднее, то его средняя квадратическая погрешность согласно составит .

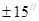Средняя квадратическая погрешность арифметического среднего М показывает, в какой мере снижается влияние случайных погрешностей при многократных измерениях.

Дата добавления: 2014-01-11