Методы определения частных порядков реакций

Как было сказано ранее, для простых химических реакций справедлив основной постулат химической кинетики, который представляет зависимость скорости реакции от концентраций исходных веществ в виде степенного ряда.

Однако очень часто и для сложных реакций используют степенную форму кинетического уравнения.

Например, для реакции

n₁ A ₁ + n₂ A ₂ = n₃ A ₃ + n₄ A ₄.

скорость реакции обычно представляют в виде

w_{V ,эксп} = k _эксп .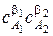

Показатели степен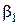и и 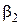называются порядками реакции по веществам A ₁ и A ₂ (В.Оствальд). Коэффициент пропорциональности в этом уравнении – это наблюдаемая, (кажущаяся, эффективная, экспериментальная) константа скорости. Она, как и порядок реакции является чисто эмпирическим параметром, в отличие от констант скорости простых реакций, которые принято называть истинными. Наблюдаемая в сложных реакциях константа скорости может зависеть не только от температуры, но и от концентраций, как реагентов, так и продуктов реакции, а также от присутствия посторонних веществ.

Порядок реакции по веществам в сложных реакциях никак не связан со стехиометрическими коэффициентами в уравнении реакции (хотя иногда формально он может и совпадать с ними). Численные значения порядков реакции могут быть любыми, в том числе нулевыми, дробными, отрицательными.

Кроме того, в отличие от простых реакций, в кинетическое уравнение сложных реакций могут входить концентрации и продуктов реакции и посторонних с точки зрения стехиометрического уравнения веществ.

Нахождение эмпирического уравнения и определение экспериментальных порядков реакции по отдельным компонентам реакционной смеси является очень важным начальным этапом в установлении наиболее вероятного механизма сложной химической реакции.

Условия для определения частных порядков реакции. Метод изолирования Оствальда

В сложных системах в реакциях участвуют большое количество реагентов. Например, в растворе химического меднения, используемом для металлизации отверстий печатных плат, присутствуют как минимум 8 компонентов. Общий вид кинетического уравнения будет следующий:

w_V = ,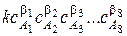

где A ₁, A ₂, … A ₈ - исходные вещества, напрямую или косвенно влияющие на скорость процесса химического меднения, и входящие в состав раствора химического меднения; 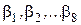- частные порядки реакции по этим веществам.

Изучить формальную кинетику такого сложного процесса - это значит определить все коэффициенты данного уравнения, то есть определить константу скорости реакции (и ее зависимость от температуры), и найти, чему равны значения порядков реакции . Рассмотрим, как определяются частные порядки реакции.

Для простоты рассмотрим реакцию, в которой имеется два исходных вещества A₁ и A₂.

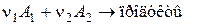
Кинетическое уравнение для такой реакции имеет вид:

w_V = .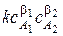

При определении частного порядка реакции по одному из компонентов, необходимо провести реакцию таким образом, чтобы концентрация другого в течение определения не изменялась. Это возможно, если использовать прием, называемый методом изолирования Оствальда или метод избытков.

Зададим начальную концентрацию одного из исходных веществ (например, A ₁) гораздо больше, чем концентрация другого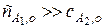

Тогда, поскольку глубина реакции х одинакова и для первого и для второго вещества, при сравнении текущих концентраций первого и второго вещества можно утверждать, что текущая концентрация первого вещества практически осталась равной его начальной концентрации и будет и дальше постоянной в течение реакции.

;

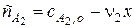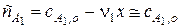
Следовательно, закон скорости можно преобразовать в такой вид:

w_V = ,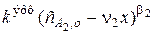

где под величиной эффективной константы скорости (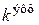) подразумевается произведение константы скорости на начальную концентрацию первого компонента в соответствующей степени

.

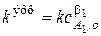Теперь можно, используя подходящий способ, определить порядок реакции по второму веществу A₂.

Дифференциальные методы определения порядка реакции

Запишем основной постулат химической кинетики для реакции, в которой применен метод изолирования Оствальда и в данной серии опытов определяется частный порядок реакции по одному из реагентов, например по A ₂:

w_v = 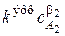. Прологарифмировав уравнение (3.6), мы получим линейную зависимость логарифма скорости от логарифма концентрации

= .

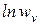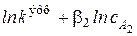Можно определить частный порядок реакции по A₂ по двум значениям скоростей реакций при двух концентрациях вещества A₂ по формуле

.

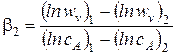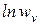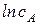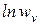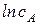А можно использовать графический вариант этого метода. Для этого строят зависимость от . Из тангенса угла наклона полученной прямой определяют порядок реакции, а из отсекаемого отрезка - константу скорости. Различные значения и могут быть получены из одной кинетической кривой, однако более надежные результаты (с учетом ошибок эксперимента) получают, используя значения начальных скоростей при разных начальных концентрациях реагентов.

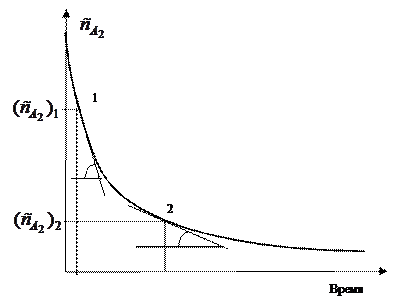В первом случае по одной кинетической кривой в разные моменты времени определяют концентрацию вещества и, проведя касательные к точке, соответствующей этой концентрации, скорость реакции.

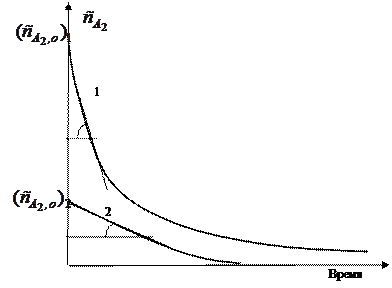
Во втором случае проводят серию опытов, отличающихся друг от друга лишь начальной концентрацией вещества A₂. Для определения частных порядков реакции в этом случае учитывают только прямолинейные начальные участки кинетических кривых, и соответственно начальную скорость реакции.

На рисунке приведена получаемая в дифференциальном способе зависимость логарифма скорости от логарифма концентрации

Описанный выше метод определения порядков реакции носит также название метода Вант-Гоффа.

Интегральные способы определения частных порядков реакции

Это способы, основанные на использовании интегральных форм кинетических уравнений. Рассмотрим метод линеаризации экспериментальных данных (или метод подстановки).

Экспериментальные данные последовательно подставляют в интегральные кинетические уравнения разных порядков и рассчитывают значение константы скорости реакции. Если для какого-то выбранного порядка константа скорости приблизительно постоянна (с учетом разброса экспериментальных данных), то изучаемая реакция имеет данный порядок. Если же рассчитанные значения константы скорости систематически убывают или возрастают, то расчет повторяют для другого порядка.

Если же ни одно из уравнений не дает удовлетворительного результата, значит порядок реакции не является целым, т.е. реакция описывается более сложным кинетическим уравнением. Метод подстановки дает надежные результаты при больших значениях степени превращения.

Другой вариант этого метода – построение графических зависимостей в координатах, где при соответствии кинетики определенному порядку зависимость должна получаться линейной.

Для реакции первого порядка это координаты: - ;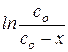

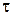Для второго (при равенстве начальных концентраций реагентов): - ;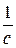

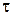Для третьего (при равенстве начальных концентраций реагентов): - .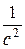

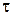Если в координатах, соответствующих одному из порядков реакции, экспериментальные точки расположились вдоль прямой линии, то изучаемая реакция имеет именно этот порядок. Одновременно из тангенса угла наклона прямой в этом случае можно получить и значение константы скорости реакции.

Известен также метод Нойеса-Оствальда. В нем используют зависимость от начальной концентрации периода превращения 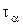исходного вещества на какую-то долю a. Из интегрального кинетического уравнения реакции, порядок которой равен 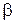(случай, когда начальные концентрации всех исходных веществ одинаковы и равны )

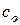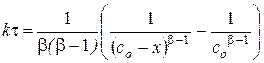
получаем:

.

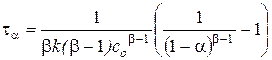Соответственно, отношение периодов 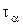для двух начальных концентраци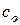й и 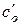равно

,

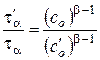Откуда после логарифмирования получаем

Или

.

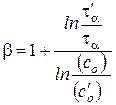Применяют также графический вариант этого метода. После логарифмирования выражения для 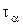получаем

.

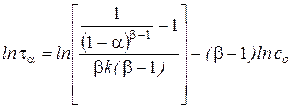В координатах 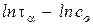этому уравнению соответствует прямая, из наклона которой можно определить порядок реакции, а из отрезка, отсекаемого прямой на оси ординат, - константу скорости.

Частным случаем метода Нойеса-Оствальда является метод определения порядка реакции по периоду полупревращения, т.е. 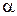= 0,5. Из уравнения тогда получаем

,

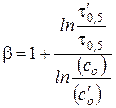графический вариант метода:

.

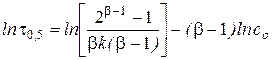Метод Нойеса-Оствальда и метод полупревращения позволяют определять любые значения порядка реакции, включая дробные и отрицательные.

Дата добавления: 2014-01-11