Несущая способность подшипников

Нс. 27.4. План скоростей в Рис. 27.5. Контактные напряжения и план скоростей в радиально-упорном подшипнике

При вращении тел качения вокруг оси подшипника на каждое из них действует центробежная сила, нагружающая дополнительно дорожку качения наружного кольца

где т — масса тела качения; w_с - угловая скорость сепаратора.

В расчетах подшипников, вращающихся с высокой частотой, необходимо учитывать центробежные силы тел качения.

Во вращающемся радиально-упорном шарикоподшипнике при действии осевой нагрузки (см. рис. 27.5) возникает гироско­пический момент на шариках, связанный с изменением на­правления оси вращения шариков в пространстве:

M_r = Jw_mw_c sin α,

где J — полярный момент инерции массы шарика, J = ρ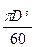

(ρ — плотность материала шарика); w_ш и ω_c — соответствен­но угловая скорость шарика при вращении его вокруг своей оси и вокруг оси вала (угловая скорость сепаратора),

Под действием гироскопического момента возникает вер­чение шариков, сопровождаемое изнашиванием поверхностей качения. Для предотвращения верчения подшипник следует нагружать такой осевой силой, чтобы

где М_т — момент сил трения от осевой нагрузки на площадках контакта шариков с кольцами (см. рис. 27.5);

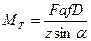
здесь F_a — осевая сила; f — коэффициент трения, f= 0,02 при высокой частоте вращения; z - число шариков в подшипнике. С учетом этих соотношений требуемая осевая сила на под­шипник для предотвращения верчения

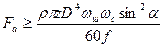
Таким образом, осевая сила, предотвращающая верчение, зависит от размера шариков, их. числа, частоты вращения подшипника и угла контакта. При высокой частоте вра­щения целесообразно использовать подшипники более легких серий (сверхлегкой, особо легкой и легкой серии) и с малы­ми углами контакта.

Основные виды повреждений подшипников. Подшип­ники невращающихся узлов часто повреждаются (образуются нмятины, намины, лунки) под действием больших статических или кратковременных динамических нагрузок (даже при тран­спортировке на дальние расстояния). Последующая работа подшипника сопровождается усиленным изнашиванием пере­мычек сепаратора и выходом подшипника из строя.

Наиболее часто подшипники повреждаются из-за усталост­ного выкрашивания беговых дорожек и тел качения под действием переменных контактных напряжений.

Для исключения повреждений беговых дорожек и тел ка­чения в течение ресурса подшипники должны удовлетворять условию прочности.

Расчет на прочность подшипников качения проводят в два этапа. Сначала рассматривают распределение нагрузки между телами качения и находят наиболее нагруженное тело (тела). Затем оценивают его прочность.

Распределение нагрузки между телами качения. Действующая на подшипник радиальная нагрузка воспринимается телами качения в зоне, ограниченной дугой не более 180° (при отсутствии натяга между кольцами и телами качения). При определении нагрузок, воспринимаемых каждым телом качения, расположенным в нагруженной зоне, исходят из следующих до­пущений: 1) радиальный зазор в подшипнике равен нулю; 2) кольца подшипника не изгибаются под действующей нагрузкой; 3) геометрические размеры тел качения и колец идеально точные.

Принимая в соответствии с указанными допущениями, что тела качения, расположенные симметрично относительно пло­скости действия нагрузки, будут воспринимать одинаковые силы, запишем условие равновесия внутреннего кольца под­шипника при действии радиального усилия F_r.

(27.1)

где Fi — силы, действующие на кольцо от i-ro тела каче­ния; i — номер тела качения; i = 0, 1, 2,..., η (рис. 27.6); γ — угловой шаг тела качения.

Рве. 27.6. К расчету распределения нагрузки и напряжений в подшип­нике

Под действием силы F_r в зонах контакта тел качения с кольцами воз­никнут упругие деформа­ции, и внутреннее кольцо переместится по направ­лению действия силы F, на величину δ₀ (см. штри­ховую линию на рис. 27.6).

Упругие деформации дорожек качения колец и тел качения в зоне кон­такта можно определить по формуле Герца (см. с. 230).

Тогда для роликоподшипников будем иметь

(27.2)
где с_р — коэффициент податливости, зависящий от модулей упругости и коэффициентов Пуассона материалов контакти­рующих деталей и кривизны их поверхностей в начальной точке контакта.

Перемещение i-ro тела качения (см. рис. 27.6) связано с перемещением центрального тела (i = 0) соотношением

(27.3)

Из равенства (27.2) следует, что δ_i/δ₀ = Fi/F₀· Учитывая это и равенство (27.3), из условия (27.1) несложно получить

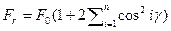
откуда

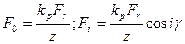(27,5)

где z — общее число тел качения; к_р — коэффициент;

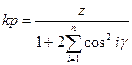
При числе роликов z = 10-20 к_р = 4,0. Обычно подшип­ники имеют некоторый радиальный зазор, и нагрузку вос­принимают тела качения на дуге, меньшей 180°, поэтому принимают k_p = 4,6.

Для шарикоподшипников задачу решают аналогично, при­нимая, что δ_i = с_шР_i^2/3. В этом Случае из расчета получают те же соотношения (27.5), в которых к_ш = 5.

Из равенств (27.5) следует, что наиболее нагружено цент­ральное тело качения.

Контактные напряжения в подшипнике. Контактные напря­жения (см. рис. 27.5) в подшипнике вычисляют по формуле Герца (см. с. 313). Тогда условие прочности по допускаемым контактным напряжениям для наиболее нагруженного тела качения в роликовом подшипнике

(27.6)

где Vi и ν₂ — коэффициенты Пуассона материалов ролика и кольца; E_t и Е₂ — модули упругости материалов ролика и кольца; ρ - приведенный радиус кривизны, 1/р = 2 {1/D + + 1/Д_В); D_B - наружный диаметр внутреннего кольца; / — эф­фективная длина (без фасок) ролика; Fq — наибольшая на­грузка на ролик, находится по формуле (27.5). Допуска­емые напряжения [σ_Η] для шарико- и роликоподшипников принимают соответственно 5000 МПа и 3000 МПа.

Статическая грузоподъемность подшипников. Допустимая нагрузка невращающегося подшипника (статическая грузоподъ­емность) назначается из условия, что остаточная деформация тел качения и колец под этой нагрузкой не превысит до­пускаемую [δ] = 10^-4D (здесь D — диаметр тела качения).

Соотношение для допускаемой нагрузки на подшипник несложно получить из условия (27.6) после подстановки в него равенства (27.5).

Опуская вывод, приведем лишь для иллюстрации структуры расчетное соотношение для статической грузоподъемности (Я) роликоподшипников с короткими цилиндрическими роликами, конических и сферических (самоустанавливающихся) ролико­подшипников при [σ_H] = 3000 МПа

C₀=22izlDcosa

ι дс i и z — соответственно число рядов и число тел каче­ния в ряду; D — диаметр ролика; α — начальный угол кон­такта.

Значения С_о для подшипников различных типов и серий даны в работе [4].

Если подшипник одновременно нагружен радиальной и осе­вой силами, то расчет ведут по приведенной нагрузке Я_о. Приведенная статическая нагрузка для радиальных и ради-ально-упорных шариковых и роликовых подшипников при­нимается большей из расчета по следующим формулам:

Rо = X₀F_r + YoF_a; Rо = F_r (27.7)

где Х_о и У_о — коэффициенты для радиальной и осевой ста­тической нагрузок, приведены в ГОСТ 18854 — 73.

Динамическая грузоподъемность подшипников. Расчет под­шипников на усталость основан на известном уравнении кривой усталости 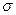^mN = k, которое часто записывают в форме

где σ — переменное напряжение цикла; N — число циклов из­менения этих напряжений до разрушения детали; т, к и с = к^1/т — постоянные величины, зависящие от свойств ма­териала и состояния поверхности детали.

Так как контактные напряжения нелинейно связаны с дей­ствующей нагрузкой [см. формулу (27.6)], то расчет удобнее вести по действующей на подшипник нагрузке R

(27.8)

где С — динамическая грузоподъемность, Н; q — показатель степени, на основании экспериментальных данных q = 3 (т = 9) для шарикоподшипников, q = 3,33 (т = 6,66) для роликопод­шипников; L— долговечность, млн. оборотов; L_h — долговеч­ность, ч.

По физическому смыслу грузоподъемность С эквивалентна радиальной нагрузке, которую подшипник может выдер­жать в течение базового числа оборотов 10^б.

На основании экспериментальных исследований установ­лены зависимости для динамической грузоподъемности, ана­логичные по структуре соотношению для С_о.

Значения динамических грузоподъемностей для подшипни­ков различных типов и серий приведены в каталогах и спра­вочниках по подшипникам.

Для расчета требуемой динамической грузоподъемности необходимо знать нагрузку на подшипник.

Приведенная нагрузка. В большинстве случаев подшипники качения подвергаются совместному действию осевой и ради­альной сил. Условия работы подшипников (по характеру нагрузок, температуре и т. д) также разнообразны.

Влияние основных эксплуатационных факторов на работо­способность подшипников учитывают введением в расчет при­веденной нагрузки — критерия подобия, который обобщает накопленный опыт по эксплуатации подшипников в различ­ных конструкциях.

По физическому смыслу приведенная нагрузка — механиче­ский эквивалент реальных условий нагружения подшипника, равноопасный по степени его повреждения с простым на-гружением радиальной силой в типичных (лабораторных) ус­ловиях.

Приведенную нагрузку для радиальных шарикоподшипни­ков и радиально-упорных шариковых и роликовых подшип­ников находят из соотношения

(27.9)

R = (XVF_r+ YF_a)K₆K_T,

где X и У— коэффициенты соответственно радиальной F_r и осевой F_a нагрузок (табл. 27.1); V— коэффициент вращения, V= 1 при вращении внутреннего кольца, V= 1,2 при враще­нии наружного кольца; K_б — коэффициент безопасности, учи­тывающий влияние на долговечность подшипников характера внешних нагрузок (табл. 27.2); К_T — температурный коэффи­циент, при температуре отпуска колец и тел качения ί < 225 °С Κ_τ=ί.

Осевые силы снижают долговечность шарикоподшипников, так как увеличивают угол контакта, вызывая скольжение шари­ков. В ответственных конструкциях производят замер осевых сил с помощью специальных силоизмерителей.

Значения коэффициентов X и Υ в табл. 27.1 даны в зави­симости от отношения F_a/(VF_r), которое влияет на распреде­ление нагрузки между телами качения. При малых значениях F_a(или до некоторого отношения ) из-за радиально-
го зазора в подшипнике имеет место повышенная неравно­мерность распределения нагрузки между телами качения. С увеличением осевой нагрузки (или при 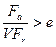) происходит выборка зазора, рабочая дуга в подшипнике возрастает и улучшается распределение нагрузки.

Таблица 27.1. Значения коэффициентов радиальной X и осевой Υ нагрузок для однорядных подшипников

Тип подшипника	Угол кон­такта	Fa/ С0	Fa/VFr < е	Fa/VFr > е	e
	a^0		X	Υ	X	Υ
		0,014				2,30	0,19
		0,028				1,99	0,22
		0,056				1,71	0,26
Шариковые радиаль-		0,084 0,11			0,56	1,55 1,45	0,28 0,30
ные		0,17				1,31	0,34
		0,28				1,15	0,38
		0,42				1,04	0,42
		0,56				1,00	0,44
Роликовые кониче-	-	—			0,4	0,4 χ ctga	1,5 χ tga
ские
Шариковые упорно-					0,66		1,25
радиальные		—	—	—	0,92		2,17
					1,66		4,67
Роликовые упорно-	_	—	_	_	tga		1,5 χ tga
радиальные
		0,014				1,81	0,30
		0,029				1,62	0,34
		0,057				1,46	0,37
Шариковые ради-		0,086 0,11			0,45	1,34 1,22	0,41 0,45
ально-упорные		0,17				1,13.	0,48
		0,29				1,04	0,52
		0,43				1,01	0,54
		0,57				1,00	0,54
	18-20				0,43	1,00	0,57
	24-26				0,41	0,87	0,68
		—			0,39	0,76	0,80
	35-36				0,37	0,66	0,95
					0,35	0,57	1,14

Таблица 27.2. Коэффициенты безопасности

Характер нагрузки	Вибрационные перегрузки	к&
Спокойная нагрузка без толчков Умеренные толчки и вибрации Сильные удары и высокие виброперегрузки	3,5 < Ja < 6,0 Jд> 10	1,3-1,8 2-3

Поэтому при отношении Fa/VFr<e осевую силу не учитывают (принимают X = 1 и У= 0), и расчет ведут лишь по радиальной нагрузке.

Значения е даны в табл. 27.1 в зависимости от отноше­ния F_a/C₀ (здесь С_о - статическая грузоподъемность подшип­ника, приведена в каталогах на подшипники).

В радиальных и радиально-упорных шарикоподшипниках угол контакта шариков под нагрузкой зависит от осевой силы. Поэтому коэффициент Υ в табл. 27.1 для этих подшипников дан в зависимости от отношения F_a/C₀.

В радиально-упорном шарикоподшипнике от действия ра­диальной силы возникает дополнительная осевая нагрузка

S = eF_r,

а в коническом роликоподшипнике

S = O,83eF_r.

Таким образом, если вал установлен на двух радиально-упорных подшипниках, то осевая нагрузка на одном из них будет складываться из внешней осевой нагрузки и допол­нительной осевой силы от другого подшипника.

Приведенная нагрузка для подшипников с короткими ци­линдрическими роликами

R = VF_rK₆K_T,

а для упорных подшипников

R = F_аKqK_t.

Для упорно-радиальных подшипников приведенную нагруз­ку определяют по формуле (27.9) при V= 1.

Если подшипники работают при изменяющейся со временем нагрузке и частоте вращения, то расчет ведут по эквивалент­ной нагрузке, равноопасной по сопротивлению усталости пе­ременному режиму нагружения:

где R_1; R₂, …, R_n — постоянные нагрузки, действующие соот-иогственно в течение L₁ L₂,..., L_n млн оборотов; L— суммар­ное число миллионов оборотов за время действия нагрузок К,, Я₂,..., R_m L= Li +L₂ +.., + Ln

Число оборотов подшипника (в млн об.) на i-м режиме (i = 1, 2, 3,..., n)

где n_i — частота вращения, об/мин; L_hi — время работы под­шипника, ч.

Если нагрузка изменяется от R_min до R_max по линейному закону, то

Дата добавления: 2014-01-11