При несимметричном нагружении

РАСЧЕТ СОЕДИНЕНИЙ

Если соединяемые элементы подвержены изгибу (случай несимметричного нагружения), то нагрузка между оди­ночными заклепочными соединениями распределяется неравно­мерно. В этом случае расчет групповых соединений сводится обычно к определению наиболее нагруженной заклепки и оценке ее прочности.

Рассмотрим соединение, содержащее п заклепок одинако­вого диаметра d под действием силы F (рис. 30.6, а). Примем для упрощения, что трение между соединяемыми деталями отсутствует и вся внешняя нагрузка передается через заклепки. Будем считать, что деформации (изгиб, сдвиг) соединяемых деталей малы по сравнению с деформациями стержней закле­пок. При этих допущениях можно полагать, что возможный взаимный поворот соединяемых деталей (листов) произойдет вокруг точки С (см. рис. 30.6, а) — центра тяжести поперечных сечений стержней заклепок. Следовательно, точку С можно использовать в качестве центра приведения внешней силы F.

В результате приведения внецентренной силы F в точку С задача расчета группового соединения сводится к определению наиболее нагруженной заклепки от действия центральной силы F (или ее осевых составляющих) и вращающего момента Т= FL

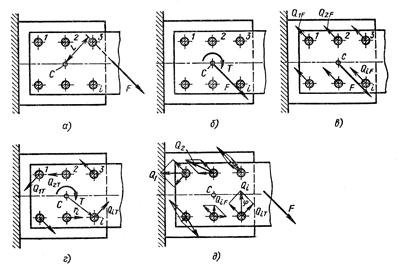
Рис. 30.6.. Расчетные схемы заклепочного соединения при несимметричной нагрузке

(рис. 30.6, б; L—расстояние от точки С до линии действия силы F, см. рис. 30.6, а).

Если соединение подвержено действию нескольких сил F_u F₂,...,F_n, то в результате приведения их к точке С оно будет нагружено главным вектором и главным моментом от этих сил.

При упругой деформации заклепок действие каждого сило­вого фактора F и Т можно рассматривать независимо. Тогда усилие, приходящееся на каждую заклепку, от силы F (рис. 30.6, в) равно, как обычно,

где i — номер заклепки, i = 1, 2,3,..., п.

Момент Т вызовет в каждой заклепке реактивное усилие 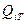, направленное перпендикулярно радиусу-вектору r_t, проведен­ному из точки С в центр сечения i-й заклепки (рис. 30.6, г). Усилие будет пропорционально перемещению сечения в резуль­тате деформации сдвига. Так как сдвиги сечений заклепок прямо пропорциональны их расстояниям до центра тяжести, то можно записать

откуда

(30.2)

Если учесть, что внешний момент Т уравновешивается моментами от усилий на заклепки, т. е.

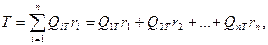
то после подстановки в это уравнение равенств (30.2) получим

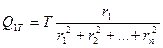
или усилие на i-ю заклепку

(30.3)

Усилие на наиболее нагруженную заклепку (рис. 30.6, д)

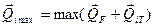
откуда модуль этого усилия

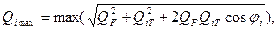
где 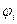- угол между векторами сил Q_F и Q_iT,

Диаметр заклепки при известном значении Q_max и ее ма­териале находим по формуле (30.1).

ГЛАВА 31

Дата добавления: 2014-01-11