
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЕщЕ действия над матрицами
|
|
|
|
а) Произведение матриц Сnk = AnmBmk определим по правилу: cij = (это правило в обиходе называется: умножение строка на столбец).
(это правило в обиходе называется: умножение строка на столбец).
Пример:  , но
, но 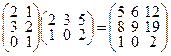 . Из определения произведения матриц ясно, что матрицы можно умножать не всегда, а только если количество элементов в строке 1ой матрицы и количество элементов в столбце 2ой матрицы совпадают. Кроме того, видно, что операция умножения матриц, вообще говоря, не коммутативна.
. Из определения произведения матриц ясно, что матрицы можно умножать не всегда, а только если количество элементов в строке 1ой матрицы и количество элементов в столбце 2ой матрицы совпадают. Кроме того, видно, что операция умножения матриц, вообще говоря, не коммутативна.
Можно отметить следующие свойства операции умножения матриц:
а1) А (ВС) = (АВ) С – ассоциативный закон;
а2 ) А (В + С) = АВ + АС – левый и
а3) (А + В) С = АС + ВС правый дистрибутивные законы.
Def: Если в линейном пространстве V над полем К, корректным образом, введена еще одна внутренняя операция, удовлетворяющая свойствам:
a⊙(х ⊗ у) = (a⊙ х)⊗ у = х ⊗(a⊙у);
х ⊗(у ⊗ z) = (х ⊗ у)⊗ z; 3) (х ⊕ у)⊗ z = х ⊗ z ⊕ у ⊗ z,
то линейное пространство над полем К называется алгеброй.
Таким образом, определив операцию умножения матриц, удовлетворяющую свойствам а1), а2), а3) мы можем говорить об алгебре матриц (для квадратных матриц).
б) Транспонирование матриц АТ Û 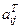 = аji.
= аji.
Пример:  .
.
Свойства операции транспонирования:
б1) (a А) Т = a АТ;
б2) (А + В) Т = АТ + ВТ;
б3) (А × В) Т = АТВТ.
в) Для матриц с комплексными элементами – операция комплексного сопряжения.  .
.
г) Для матриц с комплексными элементами – операция эрмитового сопряжения. 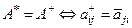 (для операции эрмитового сопряжения, математики чаще употребляют значок А *, а физики А +).
(для операции эрмитового сопряжения, математики чаще употребляют значок А *, а физики А +).
Свойства операции эрмитового сопряжения:
г1) 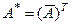 ; г2)
; г2) 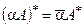 ; г3)
; г3)  ;
;
г4) 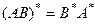 ; г5)
; г5) 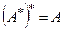 .
.
Примеры:  ;
; 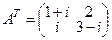 ;
; 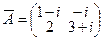 ;
;  .
.
Элементы а 11, а 22, …, ann – называются диагональными (главными диагональными) элементами матрицы.
Если " i > j aij = 0 матрица называется матрицей нижнего треугольного вида, если " i < j aij = 0 – матрицей верхнего треугольного вида:
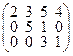 ;
;  .
.
нижний верхний
треугольный треугольный
вид вид
Примечание: Если А * = А, то матрица называется эрмитовой (самосопряженной).
В вещественном пространстве матрица А, удовлетворяющая условию: ААТ = АТА = Е называется ортогональной, а комплексном пространстве – унитарной.
РАЗДЕЛ 2. Евклидовы и унитарные пространства
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 474; Нарушение авторских прав?; Мы поможем в написании вашей работы!