Свойства определителей

6°. det A = det A^T.

◀ . ▶

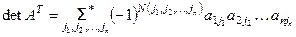Из этого свойства следует, что строки и столбцы в определителе равноправны. И все свойства для столбцов будут справедливы для строк и наоборот. Все последующие свойства сформулированы для столбцов матрицы, но * у слова столбец означает, что вместо этого слова можно написать слова строка.

7°. Если один из столбцов* определителя равен нулю, то определитель равен нулю.

◀ j(x ₁, …, θ, …, x_n) = j(x ₁, …, 0× х_k, …, x_n) = 0×j(x ₁, x ₂, …, x_n) = 0. ▶

8°. .

◀ j(x ₁, x ₂, …, x_k´ + x_k, …, x_n) = j(x ₁, x₂, …, x_k´, …, x_n) + j(x ₁, x ₂, …, x_k, …, x_n). ▶

9°. Общий множитель в столбце * определителя можно выносить за знак определителя.

◀ j(x ₁, x ₂, …, a x_k, …, x_n) = aj(x ₁, x ₂, …, x_k, …, x_n). ▶

10°. Если в определителе поменять два столбца * местами определитель поменяет знак.

◀ j(x ₁, …, x_e,…, x_m, …, x_n) = – j(x ₁, …, x_m, …, x_e, …, x_n). ▶

11°. Определитель, имеющий два равных столбца * равен нулю.

◀ Действительно, если поменять местами два столбца, то det A не изменится, ибо они одинаковы, а с другой стороны det A поменяет знак из-за антисимметричности. Следовательно, det A = 0. ▶

12°. Если столбцы* матрицы линейно зависимы, то det A = 0.

◀ Пусть х ₁ = 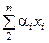. Тогда j(x ₁, x ₂, …, x_n) =

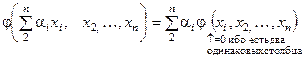= = 0. ▶

Если в матрице A_{m ´ n} зафиксировать к строк и к столбцов (k ≤ min(m, n)), то определитель k -порядка матрицы из элементов A_{m ´ n}, стоящих в выбранных строках и столбцах называются минором k -порядка.

Если у det A порядка n, вычеркнуть i -ю строку и j -й столбец, то оставшиеся элементы образуют матрицу (n – 1) порядка. Ее определитель – минор (n – 1)^го порядка и обозначается M_ij, а величина A_ij = (–1) ^{i + j} M_ij называется алгебраическим дополнением к элементу а_ij.

13°. .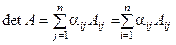

◀ =

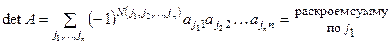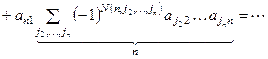
I. ;

II.

;

….. ….. ….. ….. ….. ….. ….. ….. ….. ….. ….. ….. ….. …..

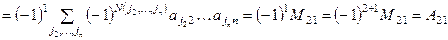n.

.

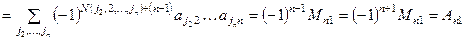Следовательно: detA= … = a ₁₁ A ₁₁ + a ₂₁ A ₂₂ + … + a_{n 1} A_{n 1}. ▶

Это все можно проделать не только для первого столбца, а и для 2^го, 3^го, …, n ^го столбцов и аналогично для строк.

14°. .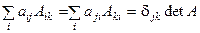

◀ . ▶

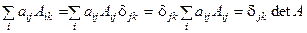15°. Определитель матрицы не изменится, если к столбцу * добавить линейную комбинацию других столбцов *.

◀ j(x ₁ + a₂ x ₂ + … + a _nx_n, x ₂, …, x_n) = j(x ₁, x ₂, …, x_n) + a₁j(x ₂, …, x_n) + a₃(x ₃, x ₂, …, x_n) +

+ a _n (x_n, x ₂,…, x_n) = j(x₁,x₂,…,x_n). ▶

16°. При умножении матрицы на a, ее определитель умножается на a ⁿ : det(A a) = a ⁿ det A.

◀ j(a x ₁, a x ₂ , …, a x_n) = a×a … aj(x ₁, x ₂, …, x_n) = a ⁿ j(x ₁, x ₂, …, x_n). ▶

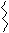
17°. Определитель произведения двух матриц произведению определителей сомножителей det A × B = det C = det A ×det B. (C = A × B Û с_ij = ).

◀ det C = = =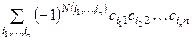

=

. ▶

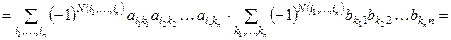
Дата добавления: 2014-01-11