Ранг матрицы. Имеется матрица Аmn порядка m´n и не все элементы ее равны 0

Имеется матрица А_mn порядка m ´ n и не все элементы ее равны 0. ($ a_ij ¹ 0).

Пусть существует минор r ^го порядка, который не равен нулю, и при этом любой минор порядка большего r равен нулю, т.е. $ M_r ¹ 0, " M_{r + i} = 0 (i =1, 2,…, n – r).

Минор M_r называется базисным минором матрицы А (он необязательно единственный), строки и столбцы, выбором которых получен минор называются базисными строками и столбцами, число r называется рангом матрицы А: r = rang A. Другими словами rang А – это наибольший порядок отличного от нуля минора этой матрицы.

6°. Теорема о базисном миноре. Строки базисного минора – линейно независимы, и любая строка матрицы А является линейной комбинацией базисных строк.

Примечание: Теорема может быть сформулирована и доказана не только для строк, но и для столбцов.

◀ 1) Пусть rang A = r. Не ограничивая общности можно считать, что первые r строк матрицы a ₁, a ₂,…, a_r – базисные. Докажем их линейную независимость.

Пусть a₁ a ₁ + a₂ a ₂ +…+ a _ra_r = q и пусть a₁ ¹ 0. Тогда a ₁ =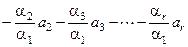, т.е. первая строка является линейной комбинацией остальных, но тогда det M_r = 0, что противоречит базисности минора M_r.

Значит a₁ = a₂ =…= a _r = 0 и, следовательно, базисные строки матрицы линейно независимы.

2) Пусть rang A = r и базисный минор M_r стоит в левом верхнем углу:

.

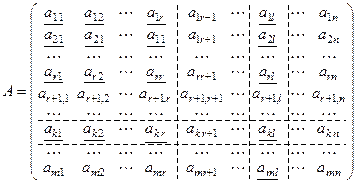Рассмотрим определитель (r + 1)^го порядка, состоящий из подчеркнутых элементов: A_{r +1}.

По условию базисности минора M_r det A_{r +1} = 0.

Разложим определитель A_{r +1} по последнему столбцу. a _{1 l} A _{1 l} + … + a_rlA_rl + a_klA_kl = 0; При этом A_kl ¹ 0 (это det M_r). Тогда .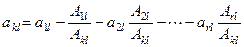

Обозначим 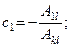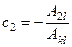; ; 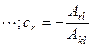A_kl – это минор M_r и не зависит ни от k, ни от l. A_il — не зависит от l (при вычитании выбрасывается). Тогда c _1, c _2, ... c_r не зависит от l, а зависит только от k. Имеем a_kl = с ₁ a _{1 l} + с ₂ a _{2 l} +...+ c_ra_rl. Последнее равенство показывает, что элементы k^й строки выражены через элементы первых r строк. ▶

Из этой теоремы следует, что:

7°. det A = 0 тогда и только тогда, когда его строки (столбцы) линейно зависимы.

8°. rang A = dimℒ(a _1, a _2, …, a_m) = dimℒ(s _1, s _2, …, s_n); a _1, a _2, …, a _m – строки; s _1, s _2, …, s _n – столбцы.

Дата добавления: 2014-01-11