Однородные системы

Преобразования, не изменяющие ранг матрицы

Следующие преобразования не изменяют ранг матрицы:

1) Транспонирование. ◀ При транспонировании определитель не меняется и поэтому, минорам равным нулю будет поставлено в соответствии миноры, равные нулю, а минорам не равным нулю будут соответствовать миноры, не равные нулю (0 «0 и ù 0 «ù 0). ▶

2) Перестановка двух строк (столбцов). ◀ Любой минор – это полилинейный антисимметричный функционал j(а ₁, а ₂, …, a_k, …, a_j, …, a_r) = – j(а ₁, а ₂, …, a_k, …, a_j, …, a_r).

Отсюда ясно, что 0 «0 и ù 0 «ù 0. ▶

3) Умножение всех элементов строки (столбца) на число C ≠ 0.

◀ j(a ₁, a ₂, …, ca_k, …, a_r) = c j(a ₁, a ₂, …, a_k , …, a_r) Þ 0 «0 и ù 0 «ù 0. ▶

4) Прибавление ко всем элементам одной строки (столбца) соответствующих элементов другой строки (столбца). ◀ Не ограничивая общности, можно считать, что к элементам 1^й строки прибавляются элементы 2^й строки

j(a ₁ + a ₂, a ₂, a ₃ , …, a_r) = j(a ₁, a ₂, …, a_r) + j(a ₁ a ₂, a ₃ ,…, a_r) = j(a ₁, a ₂,…, a_r). ▶

5) Вычеркивание нулевой строки (столбца). ◀ Включение в систему векторов нулевого вектора или выбрасывание нулевого вектора не изменяет dimℒ(a ₁, a ₂ ,…, a_r). ▶

6) Вычеркивание строки (столбца), являющейся линейной комбинацией остальных.

◀ Достаточно воспользоваться свойствами 3), 4) и 5). ▶

Рассматривается однородная система линейных уравнений с n- неизвестными:

Ах = 0 х (х _1, x ₂, …, x_n).

9°. Если rang A = n, то система имеет только тривиальное решение (х ₁ = x ₂ = …= x_n = 0);

Если rang A < n, то система кроме тривиальных имеет и не тривиальные решения.

◀ Запишем систему Ах = 0 как линейную комбинацию столбцов: x ₁ S ₁ + x ₂ S ₂ +…+ x_nS_n = 0.

1) rang A = n Þ столбцы S ₁, S ₂, …, S_n линейно независимы х ₁ = x ₂ = …= x_n = 0 (как коэффициенты тривиальной линейной комбинации линейно независимых векторов).

2) rang A = r < n Þ S ₁, S ₂, …, S_n – линейно зависимы Þ $ ненулевой набор х ₁, x ₂,…, x_n, такой что x ₁ S ₁ + x ₂ S ₂ +… + x_nS_n = 0. ▶

10°. Если с ⁽¹⁾ и с ⁽²⁾ два различных решения однородной системы Ах = 0, то "a₁, a₂ÎК a₁ с ⁽¹⁾ + a₂ с ⁽²⁾ тоже решение той же системы.

◀ Справедливость этого утверждения следует из известного свойства матриц

А (a₁ с ⁽¹⁾ + a₂ с ⁽²⁾) = a₁ А с ⁽¹⁾ + a₂ Ас ⁽²⁾ = 0. ▶

По сути дела теперь можно утверждать, что множество решений однородной системы линейных уравнений образует линейное пространство L.

11°. Размерность пространства L решений линейной однородной системы уравнений Ах = 0 с n -неизвестными удовлетворяет соотношению: dim L = n – rang A.

◀ Пусть rang A = r и S ₁, S _{2, …,} S_r – базисные столбцы матрицы А.

Записав систему Ах = 0 в виде x ₁ S ₁ + x ₂ S ₂ +…+ x_rS_r = – x_{r +1} S_{r+ 1} – x_{r +2} S_{r +2} –… – x_nS_n, отметим, что по набору x_{r +1}, x_{r +2}, …, x_n, всегда, и притом однозначно, находятся x ₁, x ₂, …, x_r (по теореме Крамера).

Пусть (c ₁, c ₂, …, c_r, c_{r +1}, …, c_n) решение системы Ах = 0. Каждому такому вектору из L поставим в соответствие вектор (c_r+1, c_r+2,…, c_n) из К_{n – r} . Это соответствие взаимно однозначно в силу сделанного выше замечания. Соблюдается это соответствие и при сложении векторов, и при умножении вектора на скаляр. Таким образом пространства L и К_{n – r} изоморфны и, следовательно, dim L = dim К_n–r = n – r = n – rang A. ▶

Доказанная только что теорема дает и способ построения базиса в L.

Записав систему Ах = 0 в виде x ₁ S ₁ + x ₂ S ₂ + … + x_rS_r = – x_{r +1} S_{r +1} – x_{r +2} S_{r +2} –… – x_nS_n.

1) Положим x_{r +1} = 1, x_{r +2} = x_{r +3}=… = x_n = 0. Найдем 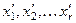(они существуют и единственны по теореме Крамера). Получим вектор – решение: е ₁(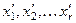,1, 0, 0,…, 0).

2) Положим: x_{r +1} = 0, x_{r +2} = 1, x_{r +3} = … = x_n = 0. Найдем 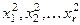. Получим:

е ₂ (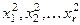,0, 1, 0, …, 0).

3) Получим:.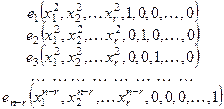

4) Построенная система векторов линейно независима и образует базис в L.

Дата добавления: 2014-01-11