Линейного оператора

Собственные векторы и собственные значения

Def: Вектор x ≠ q линейного пространства V называется собственным вектором линейного оператора А если $l₀Î K такое что Ах = l₀ х. Число l₀ называется собственным значением соответствующим собственному вектору x.

13°. Если V ₁– одномерное инвариантное подпространство оператора А то каждый x ≠ q и х Î V ₁ является собственным вектором оператора А и, притом, с одним и тем же собственным значением.

14°(обратное). Если x собственный вектор А то ℒ(x) инвариантно относительно оператора А.

◀ 1)₁₃ V ₁ – одномерное подпространство с базисом { e }: " х Î V ₁ Þ х = a е Þ Aх = Ае a = a Ае = a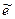= l х Î V ₁ (любой x из V ₁ собственный) Þ Aх = l х.

2)₁₃ Если Aх ₁= l х ₁Þ Пусть х ₂ = a х ₁ Þ Aх ₂ = A (a х ₁) = a Ах ₁ = al х ₁= la х ₁ =l х ₂ (для всех x одно и тоже собственное значение).

3)₁₄ Пусть Aх = l х. Рассмотрим ℒ(x):

" у Îℒ(х) Þ у = a х Þ Ау = А a х = a Ах = al х = b х Îℒ(х). ▶

Задача. Найти собственные значения и собственные векторы линейного оператора А.

Пусть x ≠ q и Aх = l₀ х, т.е. x – собственный вектор оператора А, а λ₀ – соответствующее ему собственное значение. Aх = l₀ х тогда Aх = l₀ х = (A – l₀ Е) х = 0 имеем однородную систему n линейных уравнений с n неизвестными. Т.к. x ≠ q, то чтобы система имела нетривиальные решения необходимо, чтобы det(A – l₀ Е) = 0:

.

Раскрывая определитель, получим многочлен n ^й степени относительно λ, который называется характеристическим многочленом оператора А: j(l).

¢ 13°. Характеристический многочлен j(l) оператора А не зависит от выбора базиса. ◀ ▶

Итак: Каждое собственное значение линейного оператора А является корнем его характеристического многочлена. Обратное утверждение справедливо в комплексном линейном пространстве и не справедливо в вещественном линейном пространстве для комплексных корней характеристического полинома.

Нахождение собственных векторов, соответствующих собственному значению λ₀ сводится к решению (нахождению ненулевых решений) системы (A – l₀ Е) х = 0.

Пример. Найти собственные значения и собственные векторы линейного оператора А с матрицей .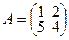

Характеристический многочлен: , тогда собственные значения оператора А: λ₁ = 6, λ₂ = –1. Найдем собственные векторы:

λ₁ = 6; ;

λ₂ = –1; .

¢ 14°. Если линейный оператор а имеет n линейно-независимых собственных векторов e ₁, e ₂, …, e_n с собственными значениями λ₁, λ₂, …, λ _n то матрица оператора А будет в этом базисе иметь вид:и наоборот: если в некотором базисе матрица имеет диагональный вид то векторы этого базиса являются собственными векторами оператора А.

15°. Собственные векторы линейного оператора А, отвечающие попарно различным собственным значениям, линейно независимы.

◀ Доказательство проведем методом математической индукции. Если собственный вектор только один, то утверждение теоремы, очевидно, справедливо.

Пусть утверждение справедливо для k – 1 векторов, т.е. что х ₁, х ₂, …, х_{k –1} собственные векторы соответствующие λ₁, λ₂, …, λ _{k –1} (различным) линейно независимы. И пусть x_k вектор собственный с собственными значениями λ _k ¹ λ _i (i = 1, 2, …, k – 1). Пусть

a₁ х ₁ + a₂ х ₂ + …+ a _{k –1} х_{k –1} + a _k х_k = 0, (*)

тогда применим к (*) оператор А: a₁ Aх ₁+…+ a _kAх_k = a₁l₁ х ₁ + … + a _{k –1}l _{k –1} х_{k –1} + + a _k l _kх_k = 0, теперь умножим (*) на λ _k: a₁l _kх ₁ + … + a _{k –1}l _kх_{k –1} + a _k l _kх_k = 0 и вычтем из первого полученного равенства второе a₁(l₁ – l _k) х ₁ + a₂(l₂ – l _k) х ₂ +… + + a _{k –1}(l _{k –1} –l _k) х_{k –1} = 0, т.к. х ₁, х ₂, …, х_{k –1} линейно независимы и λ _k ¹ λ _i получаем: λ₁ = λ₂ = … = λ _{k –1} = 0, подставляя в (*) получим λ _k = 0, т.е. λ₁= λ₂ = … = λ _k = 0 и следовательно х ₁, х ₂, …, х_{k –1} – линейно независимы. ▶

Таким образом:

16°. Если линейный оператор имеет n различных собственных значений, то, отвечающие им собственные векторы образуют базис и в этом базисе матрица оператора имеет диагональный вид.

Дата добавления: 2014-01-11